|
|
本综述来自香港中文大学Pheng-Ann Heng、西湖大学李子青实验室和浙江大学陈广勇团队,对现有的扩散生成模型进行了全面的回顾。文章GitHub链接:https://github.com/chq1155/A-Survey-on-Generative-Diffusion-Model
本文首先提出了diffusion model改进算法的细化分类与深度解析,同时对diffusion model的应用进行了系统的回顾,最后率先汇总领域内benchmarks。这也促进了后续工作《Diffusion Models: A Comprehensive Survey Of Methods and Applications》在9.7之后的改进

文章链接:https://arxiv.org/abs/2209.02646
0. Abstract
深度学习在生成任务中显示出巨大的潜力。生成模型是类可以根据某些隐含的参数随机生成观察结果的模型。最近,扩散模型凭借其强大的生成能力,成为生成模型的一大热门。除在计算机视觉、语音生成、生物信息学和自然语言处理领域的应用外,更多的应用将在这一领域得到探索。然而,目前的生成模型面临四大问题,即生成过程缓慢、数据处理类型单一、似然优化、模型降维,据此,有许多强化的工作近些年被陆续提出。本调查对扩散模型领域进行了总结。作者首先阐述了两个标志性工作的主要问题--DDPM(Denoising Diffusion Probabilistic Model) 和DSM(Denoising Score Match)。然后,文章介绍了一系列加快扩散模型的先进算法--训练方式、免训练采样、混合模型和分数与扩散统一;更多种类数据的处理--离散空间、连续空间、受限制的空间;似然的优化—改进ELBO、减小变分差。关于现有的模型,作者还对相同NFE提供了不同模型的FID得分、IS和NLL的基准。此外,作者还介绍了扩散模型的应用,包括计算机视觉、序列建模、音频、AI for Science。最后,作者也对这一领域进行了总结,并提出了局限性和进一步的方向。
1. Introduction
深度生成模型例如,VAE、EBM、GAN、归一化流和扩散模型已经创造人类无法正确区分的样本,显示出巨大潜力。作者专注于基于扩散原理的生成模型。它不需要像VAE那样对齐后验分布。VAE,像EBM那样处理无法直接表达的分区函数。训练额外的判别器(如GAN),或施加网络约束(如归一化流)。由于上述优点,基于扩散的方法已经引起了计算机视觉、自然语言处理和图分析的广泛关注。然而,目前仍然缺乏扩散模型的研究进展的系统分类和分析。扩散模型的进展提供了可操作的描述模型的概率参数化,有足够理论支持的稳定训练程序,统一的损失函数设计,具有高度的简单性。扩散模型旨在将先验数据分布转化为随机噪声,然后再一步一步地修正转换重建一个全新的样本。近几年来,扩散模型在计算机视觉(CV)生物信息学和语音处理显示出了巨大潜力。例如,Denoised Diffusion GANs产生了高分辨率的假图像,只用了只需四个采样步骤就能击败GAN。Luo等人首先使用蛋白质特征的DDPMs,在原子分辨率上生成了抗体CDR序列和结构。Wavegrad以恒定的代数步骤生成了高保真的音频样本,其性能超过了现有的基于GAN的音频生成模型。受迄今为止扩散模型在CV、生物信息学和语音处理领域的启发,将扩散模型应用于将扩散模型应用于其他领域的生成相关任务,将是一条利用强大的生成模型的有利途径。但是,扩散模型与生成对抗模型相比,有一个固有的缺点,即大量的采样步骤和较长的采样。这是因为使用马尔科夫核的扩散步骤只需要微小的扰动,这导致了大量的扩散。同时,可操作的模型在推理过程中需要相同数量的步骤推理过程中。因此,它需要成千上万的步骤来对随机噪声进行采样噪声,直到它最终改变为高质量的数据与先验数据相似。因此,很多工作都希望加快扩散过程,同时提高采样质量 。例如,DPM-solver就利用了ODE的稳定性来生成样本在10个步骤内生成较高质量的样本 。ES-DDPM成功地将轨迹学习与VAE,实现了对扩散模型的高速采样。扩散模型的高速采样。同时,扩散模型还面临着处理数据类型单一,最大似然优化和模型降维的问题,对于每个问题,文章根据解决办法提出了详细的分类。

图1. 在这个图中,我们为每一类生成模型提供了一个直观的机制产生式模型的直观机制。(a) 生成式对抗网络(GAN); (b) 基于能量的模型(EBM); (c) 变量自动编码器(VAE); (d) 归一化流(NF); (e)扩散模型(diffusion model)
因此,基于广泛的应用以及对算法改进的多角度思考分类,本综述的核心贡献如下:
- 总结了本质上的数学表述和扩散模型领域的基本算法的推导,包括统一框架内方法的制定、训练策略和采样算法。
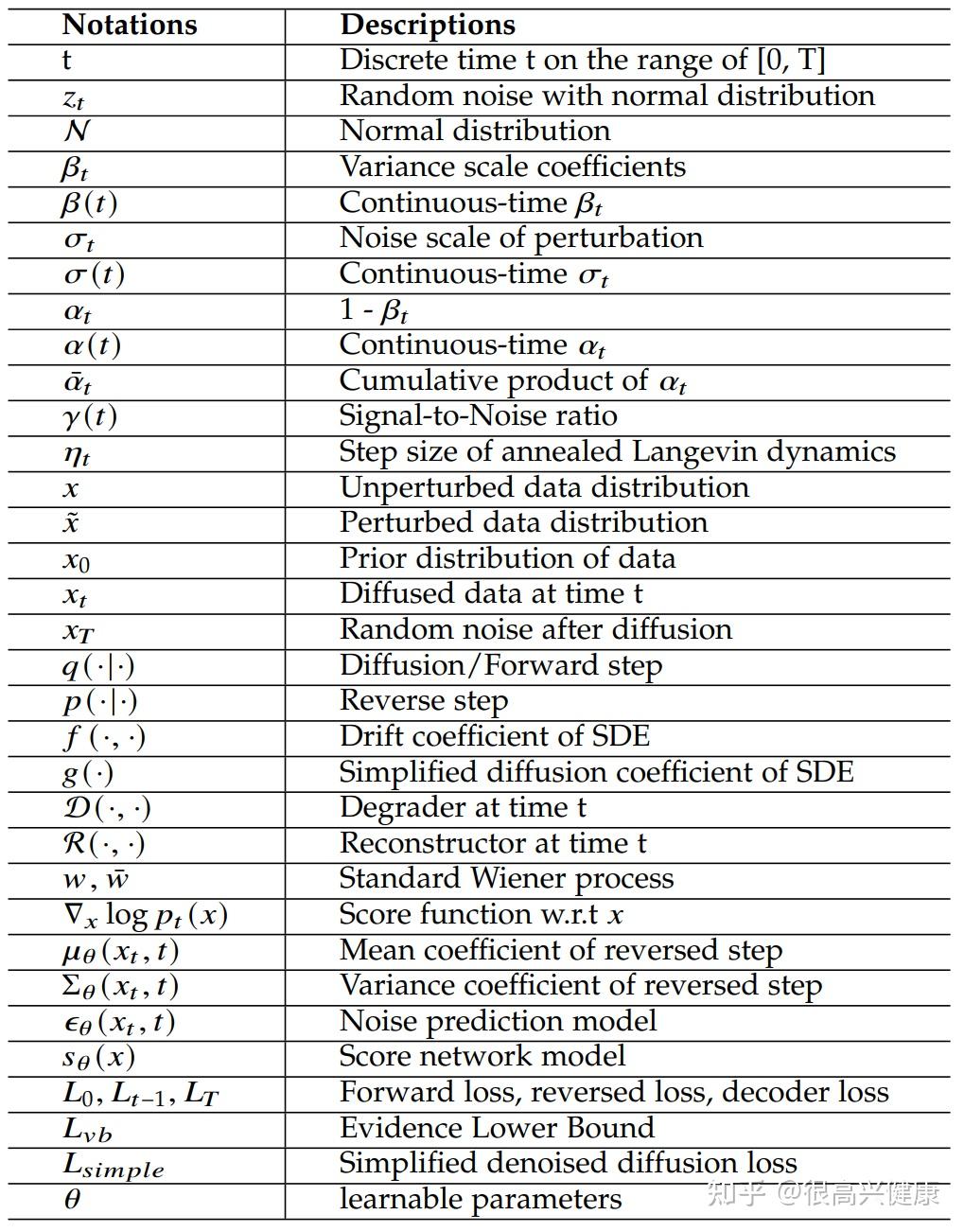
- 提出最新的扩散算法改进工作的分类,并将其划分为四类:模型加速、多元数据处理、似然优化、模型降维。
- 提供广泛的扩散模型在计算机视觉、自然语言处理、生物信息学和语音处理上的应用,包括领域专业问题的提出、相关数据集、评估指标、下游任务,以及一系列的基准。
- 阐明当前模型的局限性和可能的关于扩散模型领域的进一步证明方向。
2. Problem Statement
2.1 概念和定义
根据扩散模型的定义,统一的框架可以被描述为两个独立的过程—即前向过程和反向的过程。每个过程有许多性质相似的步骤组成,分别为前向步骤和反向步骤,对于过程中的任意时间t,模型的整体可以被表述为
(离散形式)
F(x,\sigma) = F_T(x_{T-1}, \sigma_T) \cdots \circ F_t(x_{t-1}, \sigma_t) \cdots \circ F_1(x_{0}, \sigma_1)
x_t = F_t(x_{t-1}, \sigma_t)
R(x,\sigma) = R_1(x_{1}, \sigma_1) \cdots \circ R_t(x_{t}, \sigma_t) \cdots \circ R_T(x_T, \sigma_T)
x_{t-1} = R_t(x_{t}, \sigma_t)
(连续形式)
F(x,\sigma) = F_{s1}(x_s, \sigma_{s1})F_{0t} \circ F_{ts}(x_{t}, \sigma_{ts}) \circ F_{0t}(x_0, \sigma_{0t})
x_s = F_{ts}(x_{s}, \sigma_{ts})
R(x,\sigma) = R_{t0}(x_{t}, \sigma_{t0}) \cdots \circ R_{st}(x_{s}, \sigma_{st}) \cdots \circ R_{1s}(x_T, \sigma_{1s})
x_{t} = R_{st}(x_{s}, \sigma_{st})
所以对于任意数据来说,经过前向过程与反向过程后得到的样本可以表示为:
\begin{aligned} \tilde{x}_0 = & \left[R_1(x_{1}, \sigma_1) \cdots \circ R_t(x_{t}, \sigma_t) \cdots \circ R_T(x_T, \sigma_T) \right] \circ \\ & \left[ F_T(x_{T-1}, \sigma_T) \cdots \circ F_t(x_{t-1}, \sigma_t) \cdots \circ F_1(x_{0}, \sigma_1) \right] \end{aligned}
\begin{aligned} \tilde{x}_0 = & \left[ R_{t0}(x_{t}, \sigma_{t0}) \cdots \circ R_{st}(x_{s}, \sigma_{st}) \cdots \circ R_{1s}(x_T, \sigma_{1s}) \right] \circ \\ & \left[ F_{s1}(x_s, \sigma_{s1})F_{0t} \circ F_{ts}(x_{t}, \sigma_{ts}) \circ F_{0t}(x_0, \sigma_{0t})\right] \end{aligned}
扩散模型作为生成模型的一种,训练目标为最大似然(MLE):
\mathbb{E}_{F(x_0, \sigma)}\left[-\log R\left(\mathbf{x}_{0}, \tilde{\sigma} \right)\right]
扩散系统中的概念与符号
2.2 问题表述
扩散模型的目的是分解特定的数据分布 p(x) ,并从随机噪声中一步步重建数据。由于中间过程是随机不稳定的,整个过程是生成的。此外,可逆的随机步骤确保了模型的广泛保真和样本质量。所以,利用扩散模型就是重建先验数据分布。可以分为两大类任务:分别是Diffusion和Score Matching。
2.2.1 Denoised Diffusion

2.2.2 Denoised Score Matching

3. Improved Algorithms
当今diffusion model面临的主要问题是采样缓慢以及计算消耗过大,也有问题如数据处理、极大似然以及模型降维。对于每个大类,文章细化分类,在描述改进思想的介绍之外,并且对类别内每篇文章进行详细的分析与宏观的分类。
3.1 模型加速
改变传统的训练方式例如扩散过程、噪声规模和数据分布,这些方案与采样无关。最近的相关研究表明,训练方案是影响学习模式和模型性能的关键因素。因此,在这一小节中,我们将模型加速的方法提升分为四类:知识蒸馏、扩散过程改进、噪声规模学习和数据分布替换。
3.1.1 训练方式改进
知识蒸馏
知识提炼是一种新兴的方法,通过将 "知识 "从具有高学习能力的复杂教师模型转移到简单的学生模型中,从而获得高效的小规模网络。因此,学生模型具备了模型压缩和模型加速方面的优势。
Salimans等人首先将核心思想运用到扩散模型的改进中,将知识从一个采样模型逐步提炼到另一个。在每一个提炼步骤中,学生模型在被训练成与教师模型一样接近地产生单步样本之前,从教师模型中重新加权。因此,在每个蒸馏过程中,学生模型可以将其采样步骤减半。遵循与DDPM相同的训练目标,采用替代的参数化方法,渐进式蒸馏模型仅用4步就达到了2.57的FID。这一核心思想被应用于文本到语音生成领域的ProDiff。ProDiff的采样质量在SOTA左右,只有2个采样步骤,而以前的SOTA DiffSpeech需要128个步骤进行采样。 沿着蒸馏路径的进一步改进包括去噪学生,其中教师模型通过最小化两个模型的样本的L2损失直接指导学生模型的采样模式。去噪学生得到的单步采样的FID分数为9.36,而渐进蒸馏法单步生成的FID分数为9.12。
扩散过程改进
扩散方案学习旨在探究不同的扩散模式对模型速度的影响。最近的研究集中在扩散步骤上。TDPM首先提出,截断扩散过程和采样过程,有利于减少采样时间,同时提高生成质量。截断模式的关键思想是在GAN和VAE等其他生成模型的帮助下生成更少的扩散数据。TDPM使用GAN以及条件传输,从随机噪声中学习隐性生成分布。与TDPM不同,Early Stop (ES) DDPM通过使用VAE生成先验数据来生成隐性分布,VAE从x_0中学习潜在空间。更为普遍的是,CCDF表明,存在一个小于T的最佳步骤,通过收缩理论使估计误差最小。除了减少步骤的捷径思想,Franzese等人将训练步骤的数量定义为一个变量,以便在探测最佳步骤的同时更灵活地训练模型。
学习噪声规模
与DDPM将噪声尺度定义为常数不同,有关噪声尺度学习效果的探索工作也引起了人们的关注,因为在扩散和抽样过程中,噪声表的学习也会被计算在内。每个采样步骤可以被看作是指向先验分布的直线上的随机行走,这表明噪声调整可能有利于采样程序。Improved DDPM首先考虑了噪声尺度的调整,其方式是在 L_{simple} 上定义增加一个 \lambda 尺度的项 L_{vlb} 。与改进的DDPM不同,San Roman等人提出了一种包含另一个噪声预测网络 P_{\theta} 的噪声估计方法,在进行祖先采样前的每一步中更新噪声尺度。因此,优化损失 L_{hybrid} 会导致学习噪声时间表。值得庆幸的是,改进的DDPM超过了DDIM的50步。此外,FastDPM和VDM对噪声标度 \alpha_t 和 \beta_t 进行了重新参数化,以直接表达与噪声标度有关的损失项,从而优化了与噪声计划有关的程序。总而言之,噪声学习引导了扩散和采样过程中的随机噪声的随机行走,导致了更有效的重建。
数据分布替换
数据分布替换主要集中于处理不同类型的数据分布。从先验分布的角度来看,D3PM将扩散算法推广到离散空间,通过定义句子和图像等离散数据来处理。
q\left({x}_{t} \mid {x}_{t-1}\right)=\operatorname{Cat}\left({x}_{t} ; {p}={x}_{t-1} \boldsymbol{Q}_{t}\right)
其中 \left[\boldsymbol{Q}_{t}\right]_{i j}=q\left(x_{t}=j \mid x_{t-1}=i\right) 定义为过渡, Cat(\cdot) 定义为 onehot 向量的分类分布。
此外,为了处理多正态分布的离散数据以及促进每个时间步长的数据 x_0 的更好预测,参数化和训练目标是:
p_{\theta}\left({x}_{t-1} \mid {x}_{t}\right) \propto \sum_{\widetilde{{x}}_{0}} q\left({x}_{t-1}, {x}_{t} \mid \widetilde{{x}}_{0}\right) \widetilde{p}_{\theta}\left(\widetilde{{x}}_{0} \mid {x}_{t}\right)
L_{\lambda}=L_{\mathrm{vb}}+\lambda \mathbb{E}_{q\left({x}_{0}\right)} \mathbb{E}_{q\left({x}_{t} \mid {x}_{0}\right)}\left[-\log \widetilde{p}_{\theta}\left({x}_{0} \mid {x}_{t}\right)\right]
此外,Cold Diffusion表明,噪声的数据分布可以通过冷扩散改进的采样设置为任何分布,以消除重建器 R (所有类型采样器的总称)的错误设计所带来的预测误差。Cold Diffusion改进型抽样是:

3.1.2 无训练采样改进
许多方法专注于改变训练和噪声安排的模式,以提高采样速度,但重新训练模型需要花费更多的计算,并导致不稳定的训练风险。值得庆幸的是,存在着一类直接用预训练的模型增强采样算法的方法,这就是所谓的免训练采样。高级免训练抽样的目标是提出一种高效的抽样算法,以更少的步骤和更高的精度从预训练的模型中获取知识。它包含四类:分析方法、隐式采样器、微分方程求解器采样器和动态规划调整。
分析方法
Bao等人首先提出了名为分析性DPM的分析方法。它通过KL-Divergence分析优化反向方差来改进DDIM。
隐式采样
如上所述,在DDPM中,生成过程和扩散过程重建原始数据分布,通常需要相同的步骤数。然而,扩散模型具有所谓的解耦特性,不需要扩散和采样的等量步骤。受生成性隐式模型的启发,Song等人提出了配备确定性扩散和跳步采样的隐式采样方法DDIM。令人惊讶的是,由于前向扩散概率密度在 [0, T] 内的任何时间 t 都保持不变,所以隐式模型没有重新训练模型的要求。DDIM使用连续过程公式解决了跳步加速问题,其形式为:
\mathrm{d} \overline{{x}}(t)=\epsilon_{\theta}^{(t)}\left(\frac{\overline{{x}}(t)}{\sqrt{\sigma^{2}+1}}\right) \mathrm{d} \sigma(t)
其中 \sigma_t 的参数为 \sqrt{1-α}/\sqrt{α} , \bar{x} 的参数为 {x}/\sqrt{α} 。此外,概率可以被视为一种Score SDE,它是由离散公式推导出来的。
\frac{{x}_{t-\Delta t}}{\sqrt{\alpha_{t-\Delta t}}}=\frac{{x}_{t}}{\sqrt{\alpha_{t}}}+\left(\sqrt{\frac{1-\alpha_{t-\Delta t}}{\alpha_{t-\Delta t}}}-\sqrt{\frac{1-\alpha_{t}}{\alpha_{t}}}\right) \epsilon_{\theta}^{(t)}\left({x}_{t}\right)
在DDIM的基础上,gDDIM将SDE框架中具有不同类型内核的隐性扩散,包括DDPM、DDIM和critically-damped Langevin diffusion(CLD)概括为DDIM家族,通过相应的ODE和SDE求解器实现了隐性扩散模型的加速。与上述不同的是,INDM 通过将非线性扩散过程归一化为线性隐空间扩散,实现了隐性机制。
微分方程求解器采样器
与传统的离散步骤的扩散方法相比,微分方程的数值公式通过高级求解器实现了更有效的采样。受Score SDE和Probability Flow (Diffusion) ODE的启发,有几项工作的核心是用先进的微分方程求解器进行高效采样,用较少的采样步骤使近似误差最小。现有的方法可以分为基于ODE和基于SDE。基于SDE的方法利用得分SDE中的公式和求解器,如Euler-Maruyama(EM)、改进的Euler和随机Runge-Kutta(RK)方法。基于ODE的方法有更广泛的选择,如Runge-Kutta、Forward Euler和线性多步法。一般来说,在采样速度和采样质量之间存在一个权衡。虽然高阶微分方程求解器具有较小的近似误差和较高的收敛阶数,但线性求解器需要较少的评估。此外,与SDEs相比,ODEs的求解更容易、更简单。因此,微分方程的选择与相关求解器的数量导致了另一种分类方式--在ODE、SDE和半线性DE领域的准确度优先和速度优先。
对于首选精度利用高阶求解器的方法,已经提出了使用高阶SDE求解器的Itô-Taylor采样方案。不同的是,该采样器应用理想导数替代,以一种巧妙的方式将分数函数参数化,避免了高阶导数计算。
还有一些方法,通过应用线性求解器和高阶求解器,如Gotta Go Fast和PNDM,来改善整个过程。它推导出一种基于的算法来实现对步长调整的方向性引导。在采样过程中,该方法将线性求解器(Euler-Maruyama方法)与高阶求解器(改进的Euler方法)相结合,采用外推技术,以较少的额外计算来加速。它可以在CIFAR-10上以150步达到小于3.00的FID分数。PNDM已经探索了不同的数值求解器可以共享相同的梯度。因此,它探索了在扩散ODE中使用3步高阶求解器(Runge-Kutta方法)后的线性多步法。此外,DPM-solver还利用了不同阶的求解器。根据经验,在所有的选择中,DPM-Solver-Fast(不同阶数求解器的混合进展)表现最好。因此,经过精心设计,一个联合的求解器交叉替代顺序可能有更好的性能。
此外,从微分方程选择的角度来看,DPM-solver和DEIS创造了一个新的观点,除了SDE和扩散ODE。他们声称,扩散ODE可以被看作是一种半线性形式,通过这种形式可以减少离散化误差。DPM-solver在CIFAR-10的50步内完成了SOTA,它可以在10步内生成高质量的图像(< 7 FID score),这是一个广泛的升级。另一方面,DEIS通过使用指数积分器,用多步PC取样法改进了数值DDIM。此外,DEIS-tAB3在5、10、15和20步内达到了CIFAR10的SOTA,相应的FID得分为15.37、4.17、3.37和2.86。因此,通过将其视为半线性结构来解决数值扩散模型,可获得最有效的采样质量。
动态规划调整
动态编程实现了对所有选择的遍历,通过记忆技巧在非常短的时间内找到优化的解决方案。与其他高效采样相比,采用动态编程的方法定位优化的采样路线,而不是设计强大的步骤,使误差最小化的速度更快。假设从一个状态到另一个状态的每条路径与其他路径有相同的KL-Divergence,Watson等人提出了一种高效采样方法,直接搜索具有最小ELBO的优化采样路线。这种方法只需要 \mathcal{O}\left(T^{2}\right) 进行计算和恢复,它探索了一种优化轨迹的新方法。然而,ELBO上的最小化有时与FID分数不匹配。受Kumar等人的启发,可微分的扩散采样器搜索(DDSS)利用重物化技巧来交换内存成本和计算时间。
3.1.3 混合模型改进
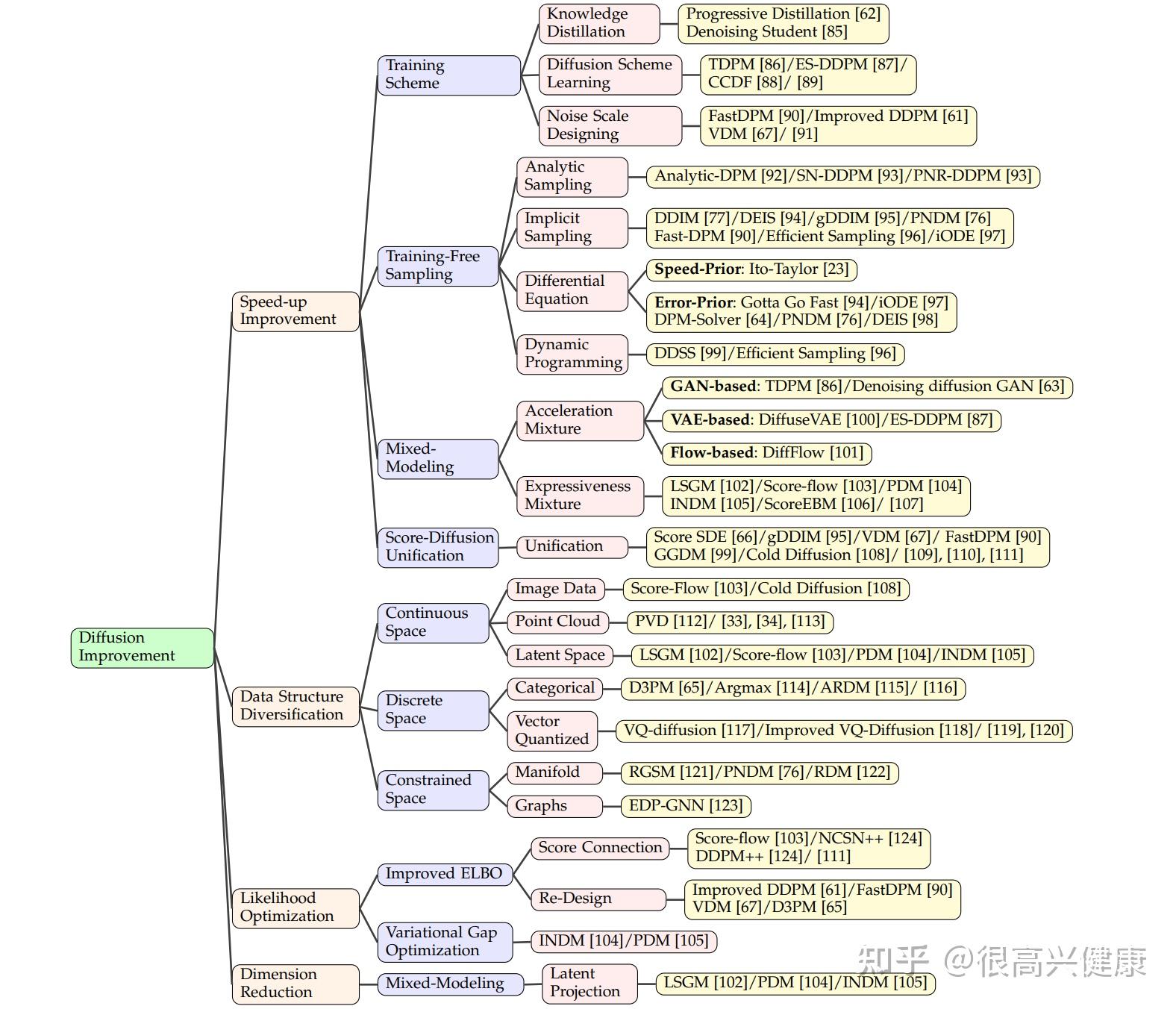
混合模型是指在扩散模型的管道中加入另一种生成模型,以利用其他模型的高采样速度,如对抗性训练网络和自动回归编码器,以及像归一化流那样的高表达能力。因此,通过将两个或更多的模型与特定的模式联合起来,提取所有的优势,进行有前途的增强,这被称为混合模型。混合建模从混合目的的角度可以分为两类:加速混合和表现力混合。
加速混合
加速混合旨在应用VAE和GAN的高速生成,在重建较少扰动的数据分布时节省大量步骤。现有的基于GAN的方法和以前一样由两部分组成:生成器负责生成样本 x^{&#39;}_{0} 以扩散到 x^{&#39;}_{t-1} ,该样本与 q(x_t|x_{t-1}) 一样接近,而判别器旨在在 x_t 的条件下与 q(x_t|x_{t-1}) 一起区分 x^{&#39;}_{t-1} 和 x_{t-1}。去噪扩散GAN成为第一个生成4步样本的DDPM相关模型,它在CIFAR-10数据集上获得了9.63的FID分数。按照类似的模式,基于VAE的模型如DiffuseVAE和ES-DDPM也适用。因为当我们使用 q(x_{t-1}|x_t, x_0) 时,在每个采样步骤中预测 x_0 需要很多时间,所以在$x_0$的生成中使用VAE,以便加速整个过程,这就是DiffuseVAE的做法。在DiffuseVAE的基础上,ES-DDPM结合了样本轨迹学习中的早期停止思想和DiffuseVAE,利用扩散的VAE样本产生的条件完成早期停止采样。
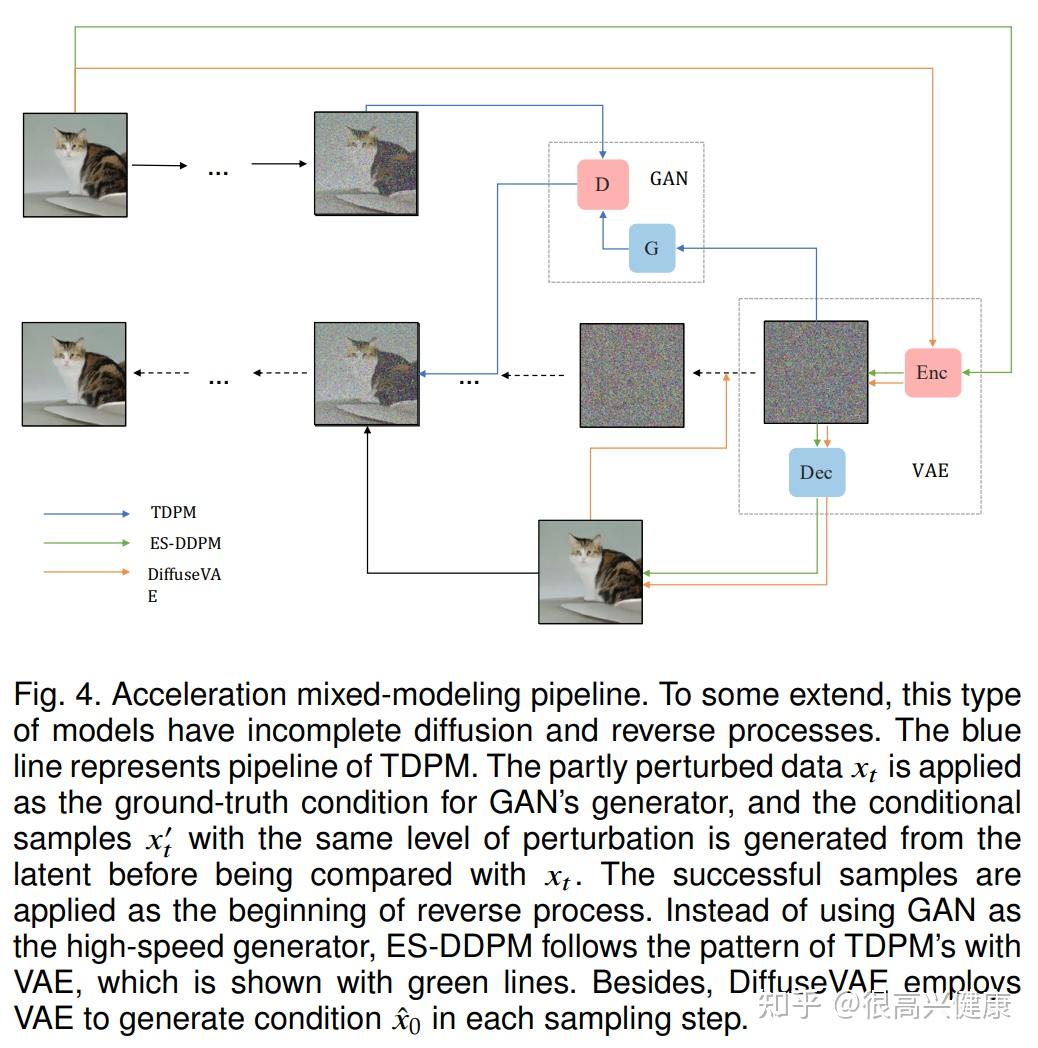
表现力混合
另一类混合建模称为表达性混合,支持扩散模型对表达数据或噪声的不同模式。至于噪声调制,DiffFlow在每个基于SDE的扩散步骤中采用流函数向前和向后,通过最小化前向过程和后向过程之间的KL-Divergence,自适应地、有效地添加噪声。与DDPM相比,DiffFlow导致了20*的速度提升,尽管由于流函数的反向传播,每一步需要更长的时间。另外一组模型利用NFs进行数据转换。基于其潜在空间(非连续数据)的训练数据使我们能够在更小的空间内学习更平滑的模型,引发更少的网络评估和更快的采样。因此,LSGM和PDM都分别使用VAE和流函数获得潜变量。此外,基于最大似然估计(MLE)的目标,LSGM与VAE共同训练了扩散过程,而PDM与可逆归一化流共同训练了分数匹配的SDE。此外,Score-Flow采用归一化流将数据分布转化为非量化场,并进行扩散过程以生成非量化样本。通过变分去量化将数据投射到去量化场,解决了连续密度和离散数据之间的不匹配问题,消除了去量化空间和离散空间之间的差距,从而提高了样本质量。
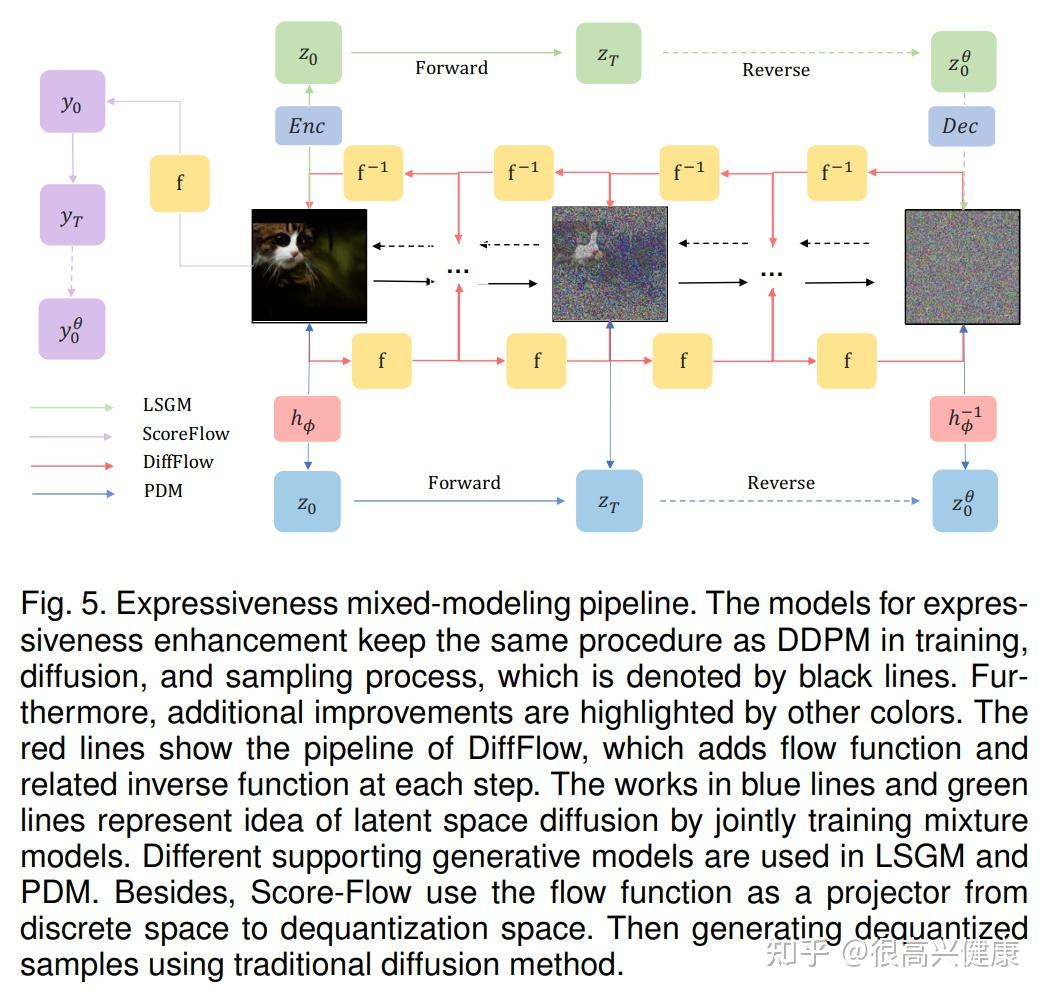
3.1.4 分数与扩散统一
有许多关于用广义的扩散模型来统一扩散模型的工作。关于广义扩散的加速方法对解决广泛的模型有很大的帮助,同时对有效的采样机制有深入的了解。另外,其他相关工作确定了扩散模型和去噪分数匹配之间的联系,这可以看作是统一的一种类型。
对于广义的观点,FastDPM和VDM完成了对噪声时间表的统一。在FastDPM中,连续时间和噪声规模之间存在着一种双射性的映射。因此,扩散和反向参数化是由$r定义的噪声尺度完成的: r: r=\mathcal{R}(t) \text { and } t=\mathcal{T}(r) 。VDM首先提出了信噪比(SNR)的参数化标准,揭示了噪声方案对扩散模型的训练和采样的影响。广义DDIM(gDDIM)将DDIM家族与根据每一步中的过渡核统一起来。
从统一的角度来看,得分SDE是将两类问题合二为一并提出统一框架的标志性工作。Gong等人,揭示了分数匹配与归一化流之间的隐藏联系,并提供了一种用流式ODEs表达分数匹配的新方法。Bortoli等人提供了一种使用Doob-h变换模拟扩散桥的变分匹配方法。
3.2 数据多样化
3.2.1 连续空间
去量化空间 & 点云数据
连续空间方法,共有两个主要类别--去量化空间和点云空间。去量化空间投影解决了连续密度和离散数据之间的不匹配问题,从而提高了样本的质量。点云数据用于三维形状生成、三维形状补全和多模态完成吸引了更多的关注,但是会遇到使用自回归编码器和归一化流采样程序不规范的问题。扩散应用于连续空间数据的扩散模型经常结合其他投影网络,如VAE和归一化流,以将各种类型的数据转化为特定的隐空间。Score-Flow采用了流函数将RGB图像投射到去量化的空间,在其上实现扩散技术以生成准确的样本。Luo等人首次提出为点云数据生成潜伏样本数据,并进行转换获得了高质量的三维形状。其他技术,如[105]、[107]、[108]以类似的方式完成形状生成和完成任务。
隐空间
隐空间数据分布经常被处理为扩散应用,因为不同类型的复杂数据结构需要一个统一的方法来归纳和分析。目前大多数方法将数据投射到连续空间,并在扩散模型的高质量生成能力的帮助下获得了可喜的性能。如EDM和antigen-diffusion。因此,隐空间处理是一种可以在新的应用领域的有益模式。
3.2.2 离散空间
文本和类别数据
对于离散空间方法,它们侧重于将不同类型的数据结构,如矢量量化数据、文本数据和分类数据等不同类型的数据结构结合到扩散模型的训练和采样,以便处理更广泛的领域任务,如文本、分割图。D3PM[91]首先将扩散算法推广到离散空间如句子和图像,其方法是定义
q\left({x}_{t} \mid {x}_{t-1}\right)=\operatorname{Cat}\left({x}_{t} ; {p}={x}_{t-1} \boldsymbol{Q}_{t}\right)
此外,为了处理多中心分布离散数据以及促进对每一时间步长的数据 _0 的更好预测,参数化和训练目标是
p_{\theta}\left({x}_{t-1} \mid {x}_{t}\right) \propto \sum_{\widetilde{{x}}_{0}} q\left({x}_{t-1}, {x}_{t} \mid \widetilde{{x}}_{0}\right) \widetilde{p}_{\theta}\left(\widetilde{{x}}_{0} \mid {x}_{t}\right)
L_{\lambda}=L_{\mathrm{vb}}+\lambda \mathbb{E}_{q\left({x}_{0}\right)} \mathbb{E}_{q\left({x}_{t} \mid {x}_{0}\right)}\left[-\log \widetilde{p}_{\theta}\left({x}_{0} \mid {x}_{t}\right)\right]
与D3PM类似,multi-nomial diffusion和ARDM将分类扩散扩展到多项式数据中,用于生成语言文本和分段地图和无损压缩.
矢量量化数据
为了处理多模型问题,矢量量化(VQ)数据将来自不同领域的数据结合到编码簿中,在自回归编码器中取得了很好的性能。Gu等人[112]首次将扩散技术应用于VQ数据,解决了VQ-VAE中存在的单向偏差和累积预测误差问题。进一步的,Xie等人[115]、Cohen等人[114]和Improved VQ-Diffusion[113]等作品完成了文本到签名的姿势生成,通过VQ-VAE生成扩散桥管道,以及推理策略的改进,通过重新定义过渡过程:
q\left(x_{t} \mid x_{t-1}\right)=\boldsymbol{v}^{\top}\left(x_{t}\right) \boldsymbol{Q}_{t} \boldsymbol{v}\left(x_{t-1}\right)
\boldsymbol{Q}_{t}=\left[\begin{array}{ccccc} \alpha_{t}+\beta_{t} & \beta_{t} & \beta_{t} & \cdots & 0 \\ \beta_{t} & \alpha_{t}+\beta_{t} & \beta_{t} & \cdots & 0 \\ \beta_{t} & \beta_{t} & \alpha_{t}+\beta_{t} & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \gamma_{t} & \gamma_{t} & \gamma_{t} & \cdots & 1 \end{array}\right]
训练方法与DDPM的相似,但采用了新的表达方案。
3.2.3 受限空间
黎曼流形
目前大多数数据结构是平面几何流形。然而,在机器人[191]、[192]、地球科学[193]以及蛋白质建模[196]等领域存在一系列定义在黎曼流形中的数据[197], 而现有的欧几里德空间方法不能很好地捕捉球体的特征。因此,最近的RDM[117]和RGSM[116]通过SDE框架将扩散技术应用于黎曼尼流形。
d\mathbf{X}_{t} = b\left(\mathbf{X}_{t}\right) \mathrm{d} t+\mathrm{d} \mathbf{B}_{t}^{\mathcal{M}}
\mathrm{d} \mathbf{Y}_{t}=\left\{-b\left(\mathbf{Y}_{t}\right)+\nabla \log p_{T-t}\left(\mathbf{Y}_{t}\right)\right\} \mathrm{d} t+\mathrm{d} \mathbf{B}_{t}^{\mathcal{M}}
相应的抽样算法被称为Geodesic随机行走(GRW)[198], [199], [200]。
X_{n+1}^{\gamma}=\exp _{X_{n}^{\gamma}}\left[\gamma \left\{b\left(X_{n}^{\gamma}\right)+(1 / \sqrt{\gamma})\left(V_{n+1}-b\left(X_{n}^{\gamma}\right)\right)\right\}\right]
与上述两种方法不同,PNDM[64]从Manifold空间中获取支持,以解决神经微分方程的采样,这实际上是一种广义的微分方程采样器[201]。
图
图正成为一个越来越热门的话题,但在扩散领域提出的工作很少。
扩散领域的工作。在EDP-GNN[118]中,图的数据在被处理之前要通过邻接矩阵进行处理。在应用于传统的离散分数匹配管道之前,通过邻接矩阵对图形数据进行处理,以捕获图的互换不变性。
3.3 似然优化
大多数变分方法[193]、[206]、[207]、[208]和二元融合方法[52]通过引入证据下限(ELBO)来训练模型,因为极大化似然是无法直接表示的。虽然最小化ELBO可以增加似然的下限,但有时相应的对数似然仍然不可观,这是因为ELBO和对数可能性之间的变分差没有被最小化。因此,一些方法[47],[86]将重点放在似然优化上,直接解决这个问题。这些解决方案可以分为两类--改进ELBO和变分差优化。
3.3.1 改进ELBO
联系打分函数
在[209]、[210]、[211]的启发下,联系打分函数在ELBO优化和分数匹配时,通过改进的分数训练解决了表示似然的问题。Score-Flow将ELBO中的前向KL发散处理为优化分数匹配损失的加权方案。Huang等人[88]将布朗运动作为一个隐变量,明确地跟踪对数似然估计,并建立了估算和加权分数匹配之间的桥梁。同样地,NCSN++通过在ELBO中引入截断因子来弥合理论上的差距。
再设计
再设计方法是通过重新设计噪声规模和训练目标来收紧ELBO。VDM和DDPM++将高级训练目标与信噪比和截断因子方面的高级训练目标,通过寻找最佳因子来优化ELBO。Improved DDPM和D3PM提出了基于ELBO的混合损失函数,并采用了加权方案。
L_{\mathrm{hybrid}}=L_{\text {simple }}+\lambda L_{\mathrm{vlb}}
L_{\lambda}=L_{\mathrm{vb}}+\lambda \mathbb{E}_{q\left({x}_{0}\right)} \mathbb{E}_{q\left({x}_{t} \mid {x}_{0}\right)}\left[-\log \widetilde{p}_{\theta}\left({x}_{0} \mid {x}_{t}\right)\right]
3.3.2 变分差优化
除了设计先进的ELBO之外,最小化变分差仍然是最大限度地提高对数可能性的一种方法。基于变分差优化[212]在VAE领域的成功,INDM应用流模型来表达变异差距,通过联合训练双向的差距,使其最小化。通过联合训练双向流动模型和潜伏空间上的线性扩散模型最小化变分差。此外,PDM通过引入VAE的编码损失来完成变异性差距的表达,最终通过集体训练,寻找唯一最优解决方案来消除差距。
3.4 模型降维
与将数据投射到潜在低维的VAE不同,计算高维数据集在训练和抽样过程中存在巨大开销。然而,现有的基于扩散的模型是基于等价空间的转换核无法实现数据降维。因此,在归一化流和VAE等降维模型的帮助下,提高模型表现力的混合建模问题显示出解决这一问题的巨大潜力。
3.4.1 混合模型改进(隐空间投影)
一些混合建模方法 训练数据投射到具有较低维度的潜空间上通过流函数和VAE Encoder进行扩散和去噪过程。LSGM [102], INDM [105] 和 PDM [104]遵循这一模式,以便在更小的空间内学习更平滑的模型 在更小的空间内学习更平滑的模型,引发更少的网络评估和快速采样[102]。此外,加权训练扩散模型的联合训练技术和基于ELBO最大化的预测模型的加权训练技术被经常采用。
4. Application
得益于生成真实样本的强大能力,扩散模型已被广泛应用于各种领域,如计算机视觉、自然语言处理和生物信息学。
4.1 计算机视觉
4.1.1 低水平视觉
CMDE根据经验比较了基于分数的扩散的扩散方法进行了比较图像数据,并引入了一个多速扩散框架。通过利用可控制的扩散速度的条件的可控扩散速度,CMDE的表现优于普通的条件性去噪估计器[59]在绘画和超分辨率任务中的FID得分。DDRM提出了一种高效、无监督的后验估计器。高效、无监督的后验采样方法,用于图像修复。在变异推理的激励下,DDRM证明了其在超分辨率、去模糊、绘画和扩散模型着色方面的成功应用。Palett进一步开发了基于扩散的统一框架,用于低级别的视觉任务,例如着色、画中画、去粗取精和修复。这项工作以其简单而普遍的想法证明了扩散模型的性能优于GAN模型。DiffC提出了一种无条件生成的方法,用一个扩散模型对损坏的像素进行编码和去噪,这显示了扩散模型在有损图像压缩中的潜力。SRDiff利用了基于扩散的单图像超级分辨率模型,并显示了有竞争力的结果。RePaint是一种自由形式的涂抹方法,它直接采用了一个预训练的扩散模型作为生成性先验,并且只用取代了反向扩散,使用给定的图像信息对未被掩盖的区域进行采样。扩散模型作为生成先验,仅通过使用给定的图像信息对未遮盖的区域进行采样来取代反向扩散。虽然没有对香草预训练的扩散模型进行修改,但该方法在极端任务下的表现超过了自回归和GAN方法在极端任务下的表现。
4.1.2 高层视觉
FSDM是一个基于条件扩散模型的几率生成框架。利用视觉变换器和扩散模型的进步,FSDM可以在测试时快速适应各种生成过程,并在几率生成下表现良好,具有强大的转移能力。CARD提出了分类和回归扩散模型,结合了基于去噪扩散的条件生成模型和预训练的条件平均估计器,以预测给定条件下的数据分布。虽然从条件生成的角度接近监督学习,并以与评价指标间接相关的目标进行训练,但CARD在扩散模型的帮助下,在不确定性估计方面呈现出强大的能力。在CLIP的激励下,GLIDE探索了以文本为条件的现实图像合成,并发现具有无分类器指导的扩散模型产生了包含广泛的学习知识的高质量图像。为了在一个平滑而有限的空间内获得富有表现力的生成模型,LSGM在变异自动编码器框架的帮助下建立了一个在潜伏空间内训练的扩散模型。SegDiff扩展了扩散模型,通过对基于扩散的概率编码器和图像特征编码器的特征图进行汇总,进行图像级别的分割。另一方面,视频扩散在时间轴上扩展了扩散模型,并通过利用典型设计的重建指导条件采样方法进行视频级生成。VQ-Diffusion通过探索离散扩散模型的无分类器指导采样和提出高质量的推理策略,改进了香草矢量化的扩散。该方法在ImageNet和MSCOCO等大型数据集上表现出卓越的性能。
4.1.3 3D视觉
《Diffusion probabilistic models for 3d point cloud generation》是一项关于基于扩散的三维视觉任务的早期工作。在非平衡热力学的激励下,这项工作将点云中的点类比为热力学系统中的粒子,并在点云生成中采用了扩散过程,从而获得了具有竞争力的性能。
PVD是一项同时进行的基于扩散的点云生成工作,但在没有附加形状编码器的情况下进行了无条件生成,同时采用了混合和点-体素表示法来处理形状。PDR提出了一种基于扩散的点云完成范式,应用扩散模型来生成基于部分观察的粗略完成,并通过另一个网络来完善生成的输出。为了处理点云去噪问题,《Score-based point cloud denoising》引入了一个神经网络来估计分布的分数,并通过梯度上升对点云进行去噪。
4.1.4 视频建模
Video diffusion将基于扩散的生成模型的进展引入视频领域。RVD采用了扩散模型来生成以上下文向量为条件的下一帧确定性预测的残差。FDM应用扩散模型来帮助长视频预测,并进行照片式的现实视频。MCVD提出了一个有条件的视频扩散框架,用于视频预测和基于遮挡帧的顺时针插值。RaMViD用三维卷积神经网络将图像扩散模型扩展到视频,并设计了一种用于视频预测、填充和上采样的调节技术。
4.1.5 医学应用
将扩散模型应用于医学图像是一个自然的选择。Score-MRI提出了一个基于扩散的框架来解决磁共振成像(MRI)重建。《Solving inverse problems in medical imaging with score-based generative models》是一个同期进行的工作,但提供了一个更灵活的框架,不需要配对的数据集进行训练。通过在医学图像上训练的扩散模型,这项工作利用了物理测量过程,并专注于采样算法,以创建与观察到的测量和估计的数据先验一致的图像样本。R2D2+将基于扩散的MRI重建和超分辨率结合到同一个网络中,以实现端到端的高质量医学图像生成。
4.2 顺序建模
4.2.1 自然语言处理
受益于扩散模型的非自回归机制,Diffusion-LM利用连续扩散的优势将噪声向量迭代去噪为词向量,并执行可控的文本生成任务。Bit Diffusion提出了一个用于生成离散数据的扩散模型,并被应用于图像标题任务。
4.2.2 时序
为了处理时间序列的估算,CSDI利用基于分数的扩散模型,以观测数据为条件。受掩蔽语言建模的启发,开发了一个自我监督的训练程序,将观察到的数值分离成条件信息和归因目标。SSSD进一步引入了结构化的状态空间模型来捕捉时间序列数据的长期依赖性。CSDE提出了一个概率框架来模拟随机动态,并引入了马尔科夫动态编程和多条件前向-后向损失来生成复杂的时间序列。
4.3 音频处理
WaveGrad和DiffWave是将扩散模型应用于原始波形生成并获得卓越性能的开创性工作。GradTTS和Diff-TTS也实现了扩散模型,但生成的是融化特征而不是原始波形。DiffVC进一步挑战了一次性多对多的语音转换问题,并开发了一个随机微分方程解算器。DiffSinger在浅层扩散机制的基础上,将普通声音的生成扩展到歌唱声音的合成。Diffsound提出了一个以文本为条件的声音生成框架,采用离散扩散模型来代替自回归解码器,以克服单向偏差和累积误差。EdiTTS也是一个基于扩散的音频模型,用于文本到语音的任务。通过对先验空间的粗略扰动,在去噪反转过程中诱发了所需的编辑。Guided-TTS和Guided-TTS2也是早期的一系列文本到语音模型,在声音生成中成功应用了扩散模型。Zero-shot diffusion将语音扩散模型与频谱域调节方法相结合,并在训练期间用未见过的声音进行文本到语音。InferGrad考虑了训练中的推理过程,并在推理步骤较少时改进了基于扩散的文本到语音模型,实现了快速和高质量的采样。SpecGrad带来了信号处理的思路,并根据调节对数梅尔谱图调整了扩散噪声的时变谱包络。Ito-TTS将文本到语音和声码器统一到一个基于线性SDE的框架中。ProDiff提出了一个用于高质量文本到语音的渐进式快速扩散模型。ProDiff没有进行数百次迭代,而是通过预测干净的数据对模型进行参数化,并采用了教师合成的Mel-spectrogram作为目标,以减少数据差异并进行清晰的预测。BinauralGrad是一个基于扩散的两阶段框架,探索了扩散模型在单声道音频合成中的应用。
4.4 AI For Science
4.4.1 分子构象生成
ConfGF是基于扩散的分子构象生成模型的早期工作。在保留旋转和平移等效性的同时,ConfGF通过Langevin动力学与物理学上的梯度场生成样本。然而,ConfGF只模拟了一阶、二阶和三阶邻域之间的局部距离,因此未能捕捉到非边界原子之间的长程相互作用。为了应对这一挑战,DGSM提出根据原子的空间接近度动态构建原子间的分子图结构。GeoDiff发现,在扩散学习过程中,模型被输入了扰动的距离矩阵,这可能违反了数学约束。因此,GeoDiff引入了一个漫游不变的马尔科夫过程,对密度进行约束。EDM进一步扩展了上述方法,纳入了离散原子特征并推导出对数可能性计算所需的方程。扭转扩散对扭转角空间进行操作,根据仅限于最灵活自由度的扩散过程产生分子构象。
4.4.2 材料设计
CDVAE探索了稳定材料生成的周期结构。为了解决稳定材料只存在于具有所有可能的原子周期性排列的低维子空间的挑战,CDVAE设计了一个基于扩散的网络作为解码器,其输出梯度导致能量的局部最小值和更新的原子类型,以捕捉取决于邻居的特定局部结合的偏好。受最近抗体建模,Refine-GNN、Energy-CDR、hierarchical docking的启发,最近的工作Antigen-diffusion开发了一个基于扩散的生成模型,明确针对特定抗原结构并生成抗体。所提出的方法对抗体序列和结构进行联合采样,并在序列-结构空间中迭代生成候选抗体。
Equivalent Protein Diffusion为蛋白质结构和序列引入了一个基于扩散的生成模型,并学习了对旋转和平移具有等价性的结构信息。ProteinSGM将蛋白质设计表述为一个图像绘画问题,并应用基于条件扩散的生成方法对蛋白质结构进行精确建模。
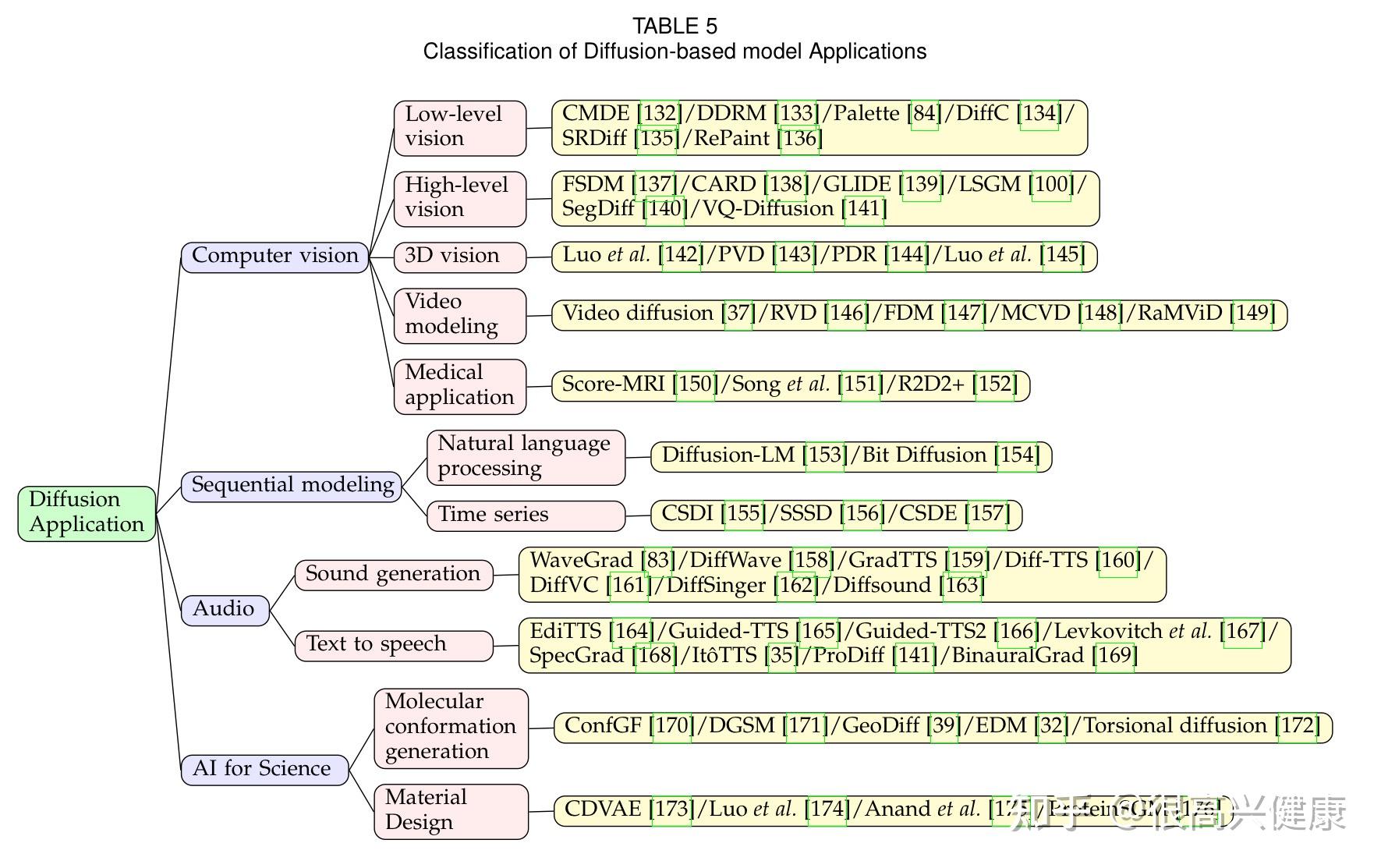
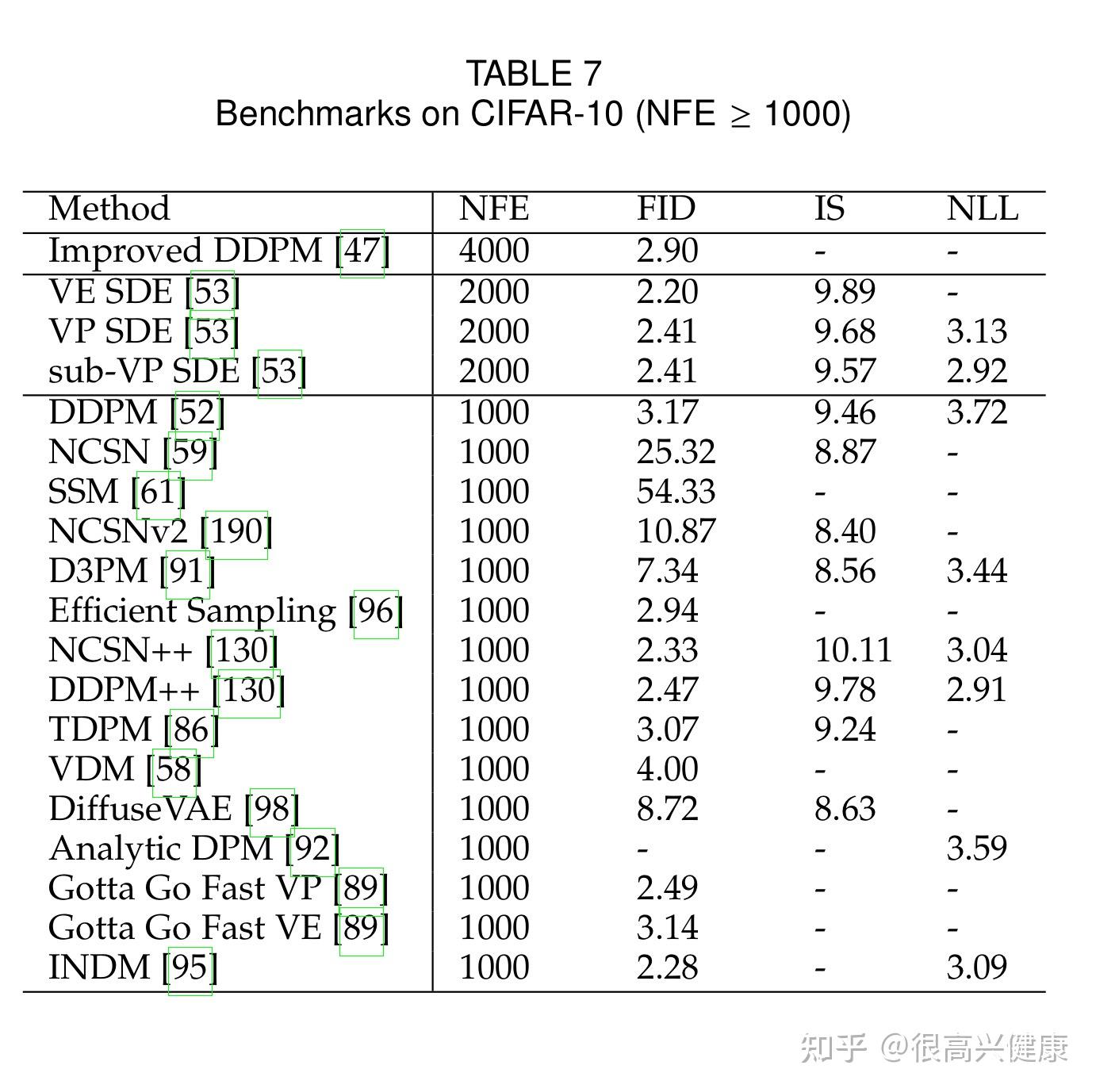
5. Benchmarks
根据各个数据集,本文率先按照NFE降序汇总了每个方法的NLL,IS与FID Score,并且定期更新。
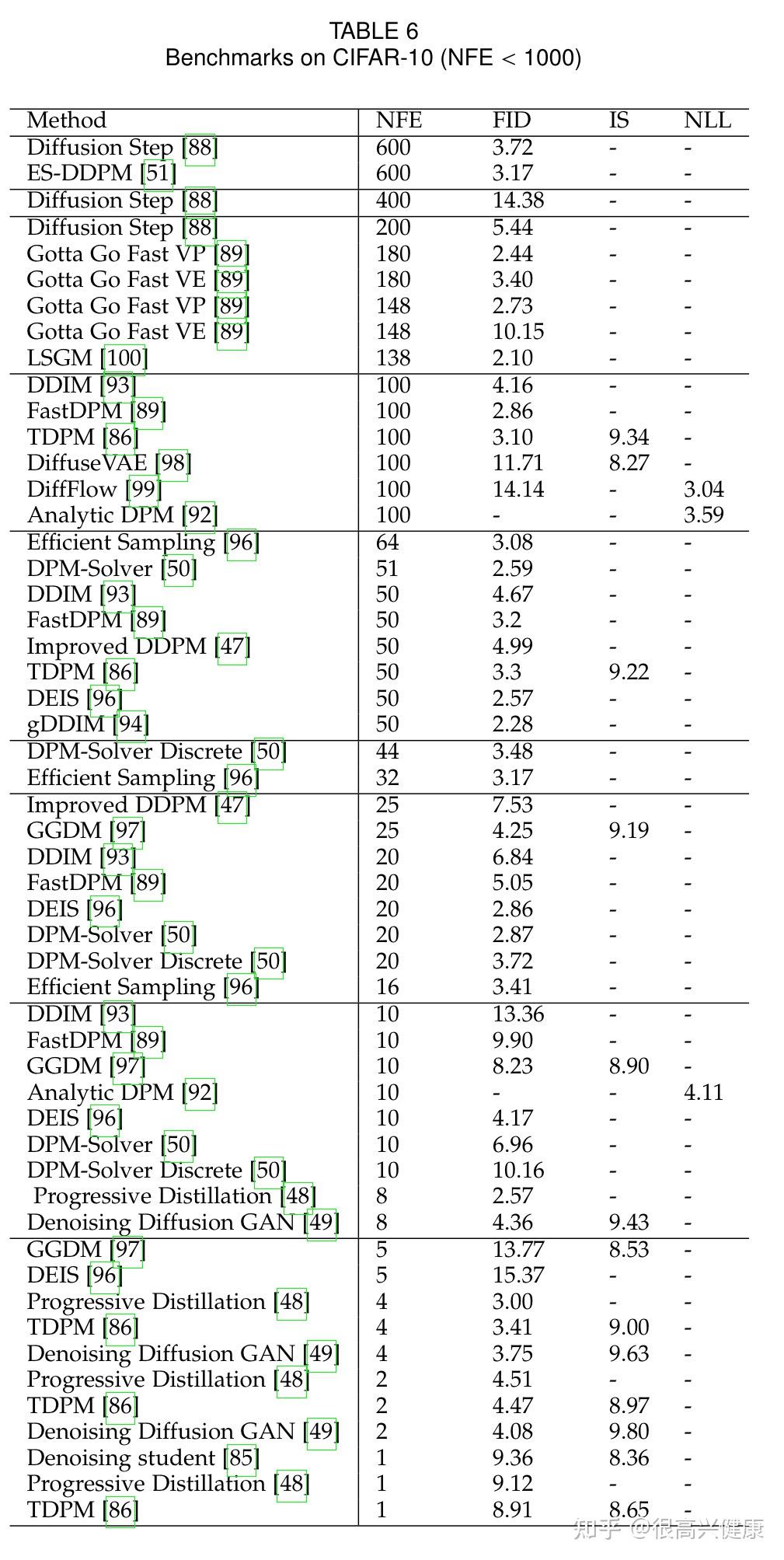
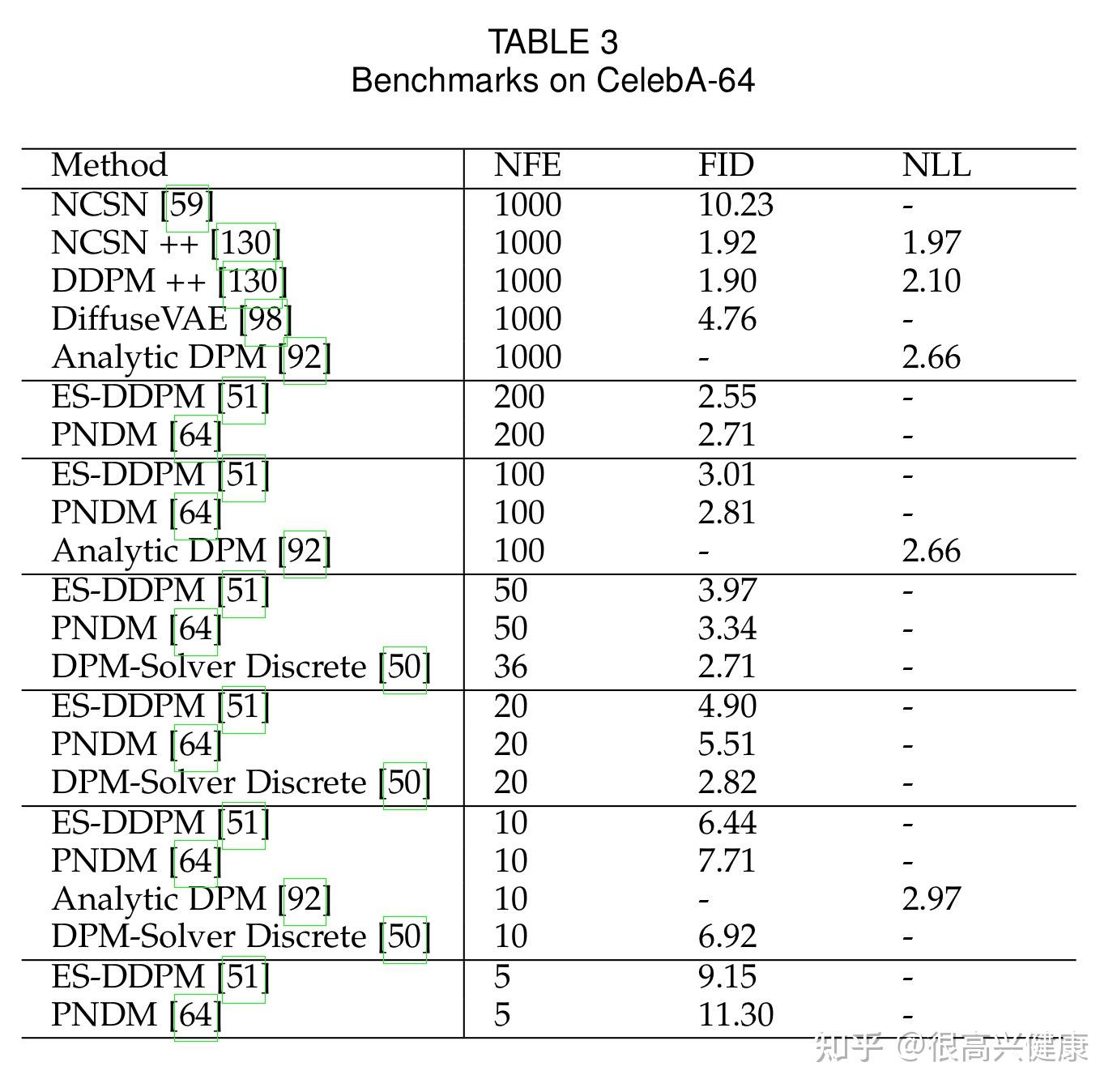
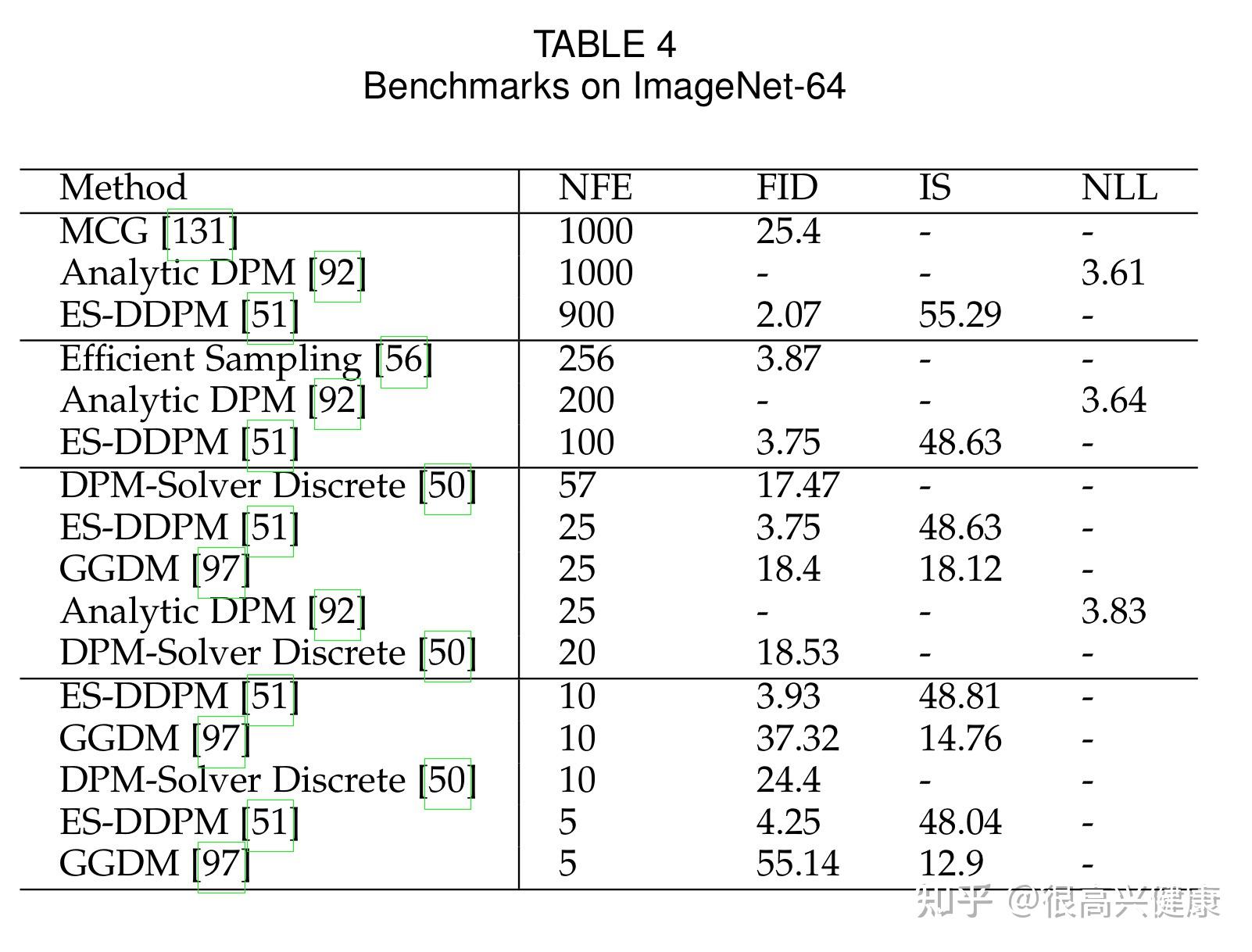
6. 结论与讨论
扩散模型正在成为一个广泛的应用领域中的热门话题。为了利用扩散模型的力量,本文利用对理论、改进算法和应用等各种态度的详细见解,对扩散模型的几个方面进行了全面和最新的回顾。我们希望这个调查能成为读者在扩散模型改进和模型提升方面的指南。
6.1 局限性
目前已经有大量的基于扩散模型的改进技术和应用领域。然而,对快速采样的更多关注导致了训练方案和原始设置的有效性降低。首先,有一个由负对数似然和证据下限之间的差异定义的变异差距。目前大多数工作都集中在优化ELBO,但忽略了对变异缺口的最小化任务,而仍有一个相对巨大的空间需要优化。其次,训练目标和评价指标性能之间不匹配。有时,较低的损失并不能带来较高的质量。因此,要探索统一这两个术语的机制,包括连接指示和度量改进。第三,现有的工作没有过多关注噪声类型和扰动核的类型。相反,高斯扰动以及作为高斯噪声的最终状态是最有可能被使用的,我们不知道高斯噪声在某些特定任务中是否合理。应该引起更多的注意。最后,模型速度和采样质量之间的权衡还不清楚,没有量化。关于定量权衡的优化任务可能为调整模型的效率提供启示。
6.2 未来发展方向
从算法和应用的角度,我们在本小节中提出了一些预期的方向。一方面,应该对不同的数据类型进行更多的尝试,包括离散空间、去量化空间和潜伏空间。同时,需要进行探索不同的最终状态噪声类型和扰动核的实验,如正态分布、伯努利分布、二项分布和泊松分布,以扩大扩散模型的多样性。此外,一个明确的损失优化机制与加速/质量权衡将导致对可控调节和更令人满意的性能产生有希望的影响。另一方面,为了获得更好的发电性能,有很多领域都采用了扩散模型。然而,目前的大多数应用仍然是肤浅的。人们期待更多针对具体问题的扩散模型,特别是针对科学问题。
特别鸣谢:十分感谢王晋东老师 @王晋东不在家 的迁移学习综述为我们的分类图绘制提供的灵感
声明:如有内容引用,烦请引用原文:《A Survey on Generative Diffusion Model》
@article{cao2022survey,
title={A Survey on Generative Diffusion Model},
author={Cao, Hanqun and Tan, Cheng and Gao, Zhangyang and Chen, Guangyong and Heng, Pheng-Ann and Li, Stan Z},
journal={arXiv preprint arXiv:2209.02646},
year={2022}
} |
|