|
|
是时候实现表达式模板求值了。
表达式求值,又名符号计算,惰性求值等等。它解决的是这样一类问题:对于一个我们常见的中缀表达式组合:
g_1\oplus g_2...\oplus g_n\tag{1}
计算机会生成非常多的中间结果,因为计算机看到的是:
\oplus(g_1,\oplus(g_2,...))\tag{2}
这样的函数调用流程,每次都会拿两个操作数,消耗一个运算符,生成中间结果,然后循环,直至运算完成。
拿我的矩阵类作实际例子,在dtor中加入打印,计算 A=A+A+A+A :
Dtor!
Dtor!
Dtor!
Dtor!虽然我们实现了移动构造,但计算过程依然创建了三个中间对象。这对于复杂代数表达式或大矩阵计算是致命的。因为对于这种情形,直接对应分量相加不需要任何中间变量:a_{i}=a_{i}+a_{i}+a_{i}+a_{i}\\但这样就要求:计算机求值时,将表达式作为整体一起求值,而不是当作多元算符的组合。 实现这种功能的技术,被称作表达式求值/符号计算/惰性求值。
简单符号计算原理
如前所述,符号计算原理是将表达式作为一个整体求值。这和平时代码流程是不一样的。平时的表达式,实际上是同一个类型不停的消耗操作数合并计算结果。而符号计算/表达式模板要求将表达式看作一个单独的类型,其中储存了计算的过程。简单来说,无论何种语言,符号计算的相关类都会储存这样一颗树:
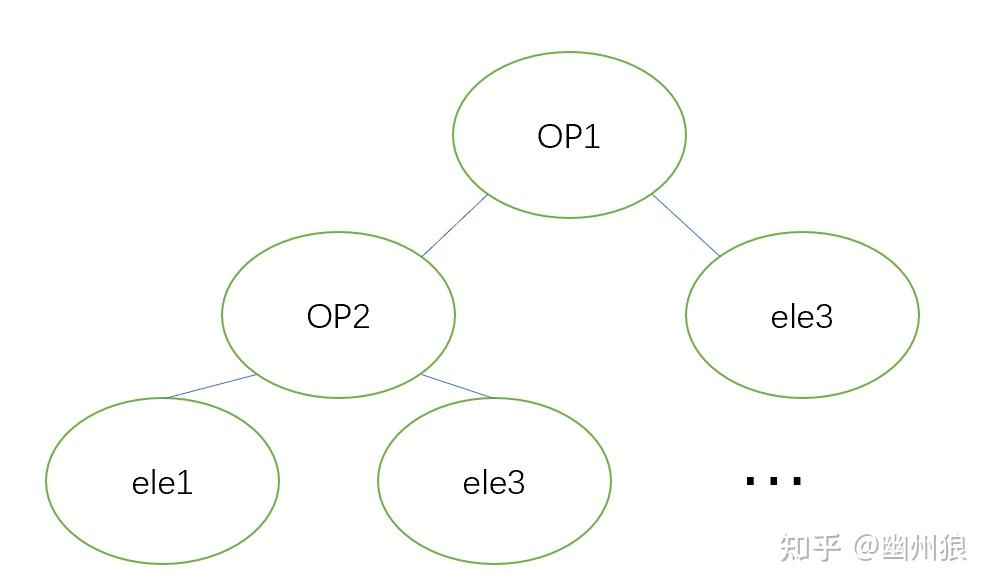
非常简单的计算图
熟悉编译器AST构造过程的很快能明白,这实际就是语法树。其实无论是当红的自动微分库ceres还是传统的mma符号计算,基础原理都是把表达式抽象成语法树后处理。所谓惰性求值就是将表达式转换为专门的类型储存起来,需要用到时,求出表达式的值。
表达式模板
符号计算原理简单,但这一切在CPP里变得不同。因为大家都知道CPP追求零开销,对于符号表达式这种东西,肯定看不上运行时构造的语法树,一定要在编译期把表达式塞进模板里面。
这种方法叫表达式模板,在标准库实现Lambda和Eigen,Boost::uBLAS这些线代库时用的非常多。我今天还没有时间实现很通用的表达式模板,就以加法为例,快速说明用表达式模板编程实现符号计算的的技巧。
如上所述,表达式模板是单独的一个类型,它在它的模板参数中储存我们的表达式:
a*b+c-d\rightarrow class<minus(add(c,mul(a,b)),d)>\tag{3}\\
对于二元运算符一般是抽象一个基类,这里我只用先只使用加法为例构造表达式模板类:
template <typename LHS, typename RHS>
class MatrixSum
{
public:
using value_type = typename LHS::value_type;
MatrixSum(const LHS &lhs, const RHS &rhs) : rhs(rhs), lhs(lhs)
{
}
value_type operator[](size_t idx) const
{
return lhs[idx] + rhs[idx];
}
template <typename T>
MatrixSum<MatrixSum<LHS, RHS>, T> operator+(const T &rhs)
{
return MatrixSum<MatrixSum<LHS, RHS>, T>(*this, rhs);
}
private:
const LHS &lhs;
const RHS &rhs;
};
这个模板类储存两个操作数的引用,当遇到加号时,生成一个新的模板,把右操作数和自己套娃到模板里面,这样就把表达式塞进模板类参数了。而[]操作符则是传递左右操作数的[]操作,类中value_type标签同样起到传递类型参数作用。这样就得到了一个将算术式编码到模板参数的类。
第二步需要改造我们的矩阵类。让矩阵的加法返回表达式模板而不是矩阵,以此启动模板计算。矩阵类也需要能从模板表达式构造出来,因为我们并没有在表达式模板中实现任何的输出函数。
template <typename T1, typename T2>
Matrix(const details::MatrixSum<T1, T2> &expr)
{
for (size_t i = 0; i < M * N; i++)
{
(*this) = expr;
}
}
template <typename T1, typename T2>
Matrix &operator=(const details::MatrixSum<T1, T2> &expr)
{
for (size_t i = 0; i < M * N; i++)
{
(*this) = expr;
}
return *this;
}
details::MatrixSum<Matrix, Matrix> operator+(const Matrix &other) const
{
return details::MatrixSum<Matrix, Matrix>(*this, other);
}这样就完成了C++中最简单的表达式惰性求值,还是用之前的例子 A=A+A+A+A ,
当代码是:
auto ccc = a + a + a + a;这时ccc的类型参数是:
details::MatrixSum<details::MatrixSum<details::MatrixSum<Matrix<4Ui64, 4Ui64>, Matrix<4Ui64, 4Ui64>>, Matrix<4Ui64, 4Ui64>>, Matrix<4Ui64, 4Ui64>>这正是我们想要的,计算式返回来一个类模板,里面的类参数是表达式本身。
从它构造矩阵或者矩阵从它赋值时,我们让他调用[]操作符,开始实际计算每一参数:
Matrix<4, 4> ccc = a + a + a + a;这次同样的在dtor中加入打印,观察构造是否生成了中间变量:
Dtor
Dtor一个中间变量都没有了,这两个dtor分别属于a和ccc。没有表达式求值能力的代码会随着表达式的复杂化构建非常多临时变量,而有表达式求值则不会。
表达式求值当然不是万能的,不然每家语言早就做进特性了。
引入表达式模板失去了编程的直观性。表达式模板写法一般需要通过某种声明和程序中普通代数式子区分开,而对其求值要使用诸如eval或者[]这类操作符实现。特别是C++中,除非详细的处理了表达式模板的功能,那么它的加入会让计算便利性下降。你需要显式的为表达式模板类构造所有以前计算式返回类型的功能。
当然,惰性求值与符号计算依然是线代库中不可缺少的一部分,我依然将在后续过程中完善目前矩阵库惰性求值功能。代码可以从github获取: |
|