|
|
引言
全球变暖的速度比有记录以来的任何时候都要快。截至目前,全球地表平均温度比 19 世纪末升高了 1.1 ℃,过去十年是有史以来最热的十年[1]。随着时间的推移,气温变暖正在改变气候,破坏自然的正常平衡。这给人类和地球上所有其他形式的生命带来了许多风险(图 1)。

图 1: 气候变化已带来诸多负面影响
气温升高导致极地冰原融化,海平面上升,淹没较低洼的沿海陆地;气候变化导致热浪、干旱、暴雨、台风等极端天气越来越频繁,这对生态体系、水土资源、人类活动与生命安全等都会造成很大的伤害;气候变化造成粮食减产,千百万人将面临饥饿的威胁;珊瑚礁、极地、高山生态系统、热带雨林、草原、湿地等自然生态系统受到严重的威胁,生物多样性受损害。
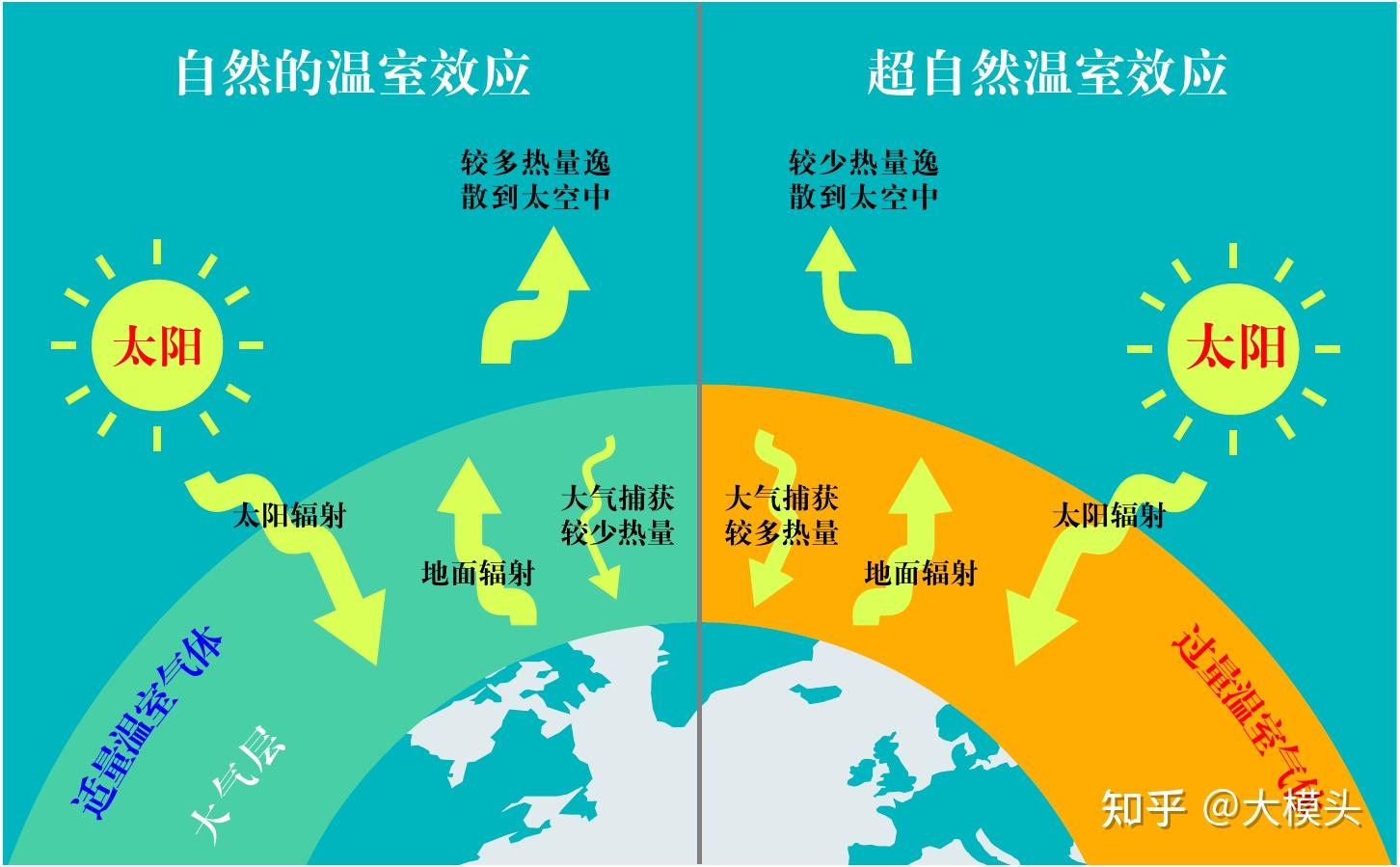
图 2: 自然的和超越自然的温室效应
大量研究表明[1,2],温室气体(特别是二氧化碳,CO2)大量排放所造成的温室效应加剧是全球变暖的主要原因。温室效应是指行星的大气层因为吸收辐射能量,使得行星表面升温的效应。由于温室效应,行星表面温度会比没有大气层时的温度要高。太阳向外的辐射主要是短波辐射,然而地面向外的辐射和大气辐射则是长波辐射。大气对长波辐射的吸收力较强,对短波辐射的吸收力较弱。白天时,太阳光照射到地球上,部分能量被大气吸收,部分被反射回宇宙。晚上地球表面以红外线的方式向宇宙散发白天吸收的热量,其中也有部分被大气吸收。大气层像覆盖玻璃的温室一样,保存了一定的热量,使得地球不至于像没有大气层的月球一样,被太阳照射时温度急剧升高,不受太阳照射时温度急剧下降。如果没有温室效应,地球就会冷得不适合人类居住。但近现代人类活动排放了大量的 CO2 等温室气体,这些温室气体将本可以逸散到太空中的红外辐射捕获并留在大气中,从而加剧了温室效应(图 2)。
问题
近一个世纪以来,全球气温不断上升。图 3 给出了 1959-2021 年以来全球地表平均温度异常[3],这个温度异常值是相对 1951-1980 年地表平均温度 14.2 ℃ 而言的。例如 2021 年的地表平均温度异常值为 0.84 ℃,这表示 2021 年的地表平均温度比 14.2 ℃ 的基准值高 0.84 ℃。

图 3: 全球地表平均温度异常
主流的科学观点认为,CO2 为首的温室气体是造成全球变暖的主要原因。工业化以前的数千年人类文明中,大气中的 CO2 浓度均保持在 280 ppm(parts per million,百万分比)左右。但由于近现代人类活动排放了大量的 CO2 等温室气体,大气中的 CO2 浓度不断升高。

图 4: 全球二氧化碳平均浓度
图 4 给出了 1959-2021 年以来全球大气 CO2 平均浓度[4],其中 2022 年的 CO2 浓度达到了 421 ppm。请根据图 3 和图 4 中的数据建立模型,回答以下问题:
- 按照目前的趋势,2050、2075 和 2100 年大气中 CO2 的平均浓度将达到多少?CO2 的浓度将在哪一年达到工业化以前的两倍(即 280 \times 2 = 560 ppm)?
- 试建立全球 CO2 平均浓度和地表平均温度异常值之间的关系,并分别预测 2050、2075 和 2100 年的地表平均温度异常。温度异常将在哪一年超出基准值 2 ℃?
模型
二氧化碳浓度预测
随着人口的不断增涨和人们对化石燃料需求的增大,地球大气中的 CO2 持续上升(图 4)。研究表明,大气中的 CO2 浓度是呈指数或超指数增长的[5,6]。考虑到人类活动所排放的 CO2 量应该是与人口数量正相关的,而人口的增长通常被认为是符合指数函数的。因此,本文使用指数函数模型对 CO2 浓度的历史数据进行了拟合,拟合结果为
C = 58.72\, \mathrm{e}^{0.0162\,(t-1959)} + 256 \\
拟合优度 R^2 = 0.9995,R^2 是衡量拟合优劣程度的统计量,其取值在 0 到 1 之间,越接近于 1 拟合效果越好。相应的拟合曲线见图 5 中的红色曲线。

图 5: 二氧化碳浓度多模型拟合
从图中不难看出,红色曲线与实际数据(空心圆点)非常吻合。作为对比,本文还使用了二次函数模型和幂次函数模型对 CO2 浓度的历史数据进行了拟合,拟合曲线见图 5。局部放大拟合曲线的末端不难发现,对于近几年数据的近似,指数函数模型要优于其它模型。
如果人类不作出任何改变,仍然执行当前的碳排放策略,那么大气中的 CO2 浓度将继续按照目前的趋势增长。这种情况下,我们可应用拟合得到的指数函数模型对未来的 CO2 浓度进行预测,结果如图 6 所示。

图 6: 二氧化碳浓度指数函数模型预测
预测结果表明,2050、2075 和 2100 年 CO2 浓度将分别达到 512.7、641.0 和 833.3 ppm。CO2 浓度将在 2060 年达到工业化以前的两倍,即 560 ppm。
地球能量平衡模型
很多科学家都认为,CO2 浓度的升高是造成全球变暖的主要原因。接下来本文将从能量平衡角度来研究 CO2 浓度与地表平均温度的关系。地球之所以具有相对稳定的温度,主要是地球从太阳短波辐射获得的能量与地球向外太空长波辐射出去的能量相互平衡的结果[7,8]。
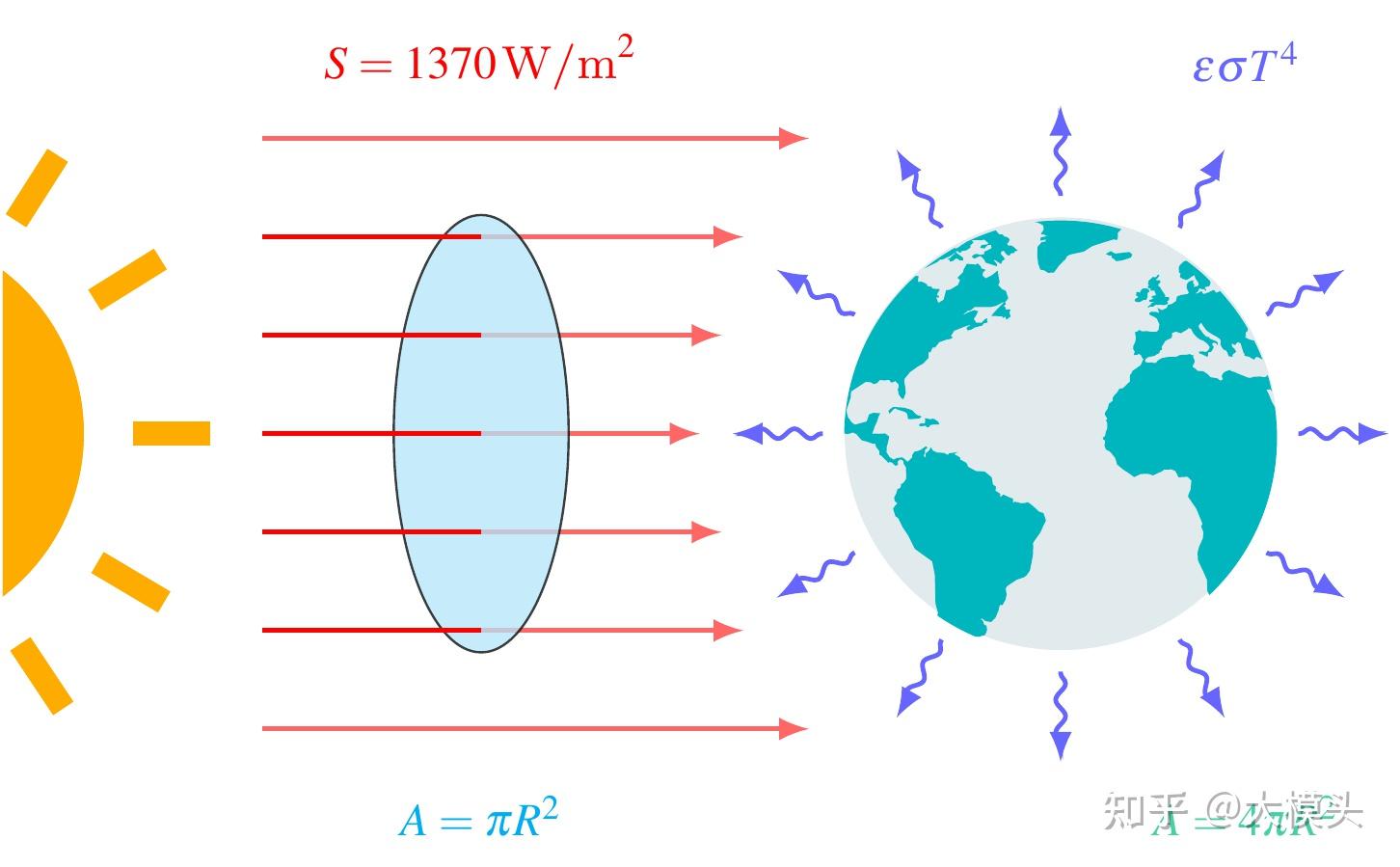
图 7: 地球能量平衡模型示意图
地球到太阳的距离平均约 1 AU (天文单位),太阳照射到地球外层垂直于光线单位面积上的辐射功率约为 S = 1370 W/m2。假设地球半径为 R,则太阳辐射给地球的功率为 S\cdot\pi R^2,其中 \pi R^2 为地球垂直于光线的有效面积。但有大约 30% 的太阳辐射会被反射回太空,即反照率约为 a = 0.3。考虑到地球的表面积为 4\pi R^2。因此,地球表面单位面积上获得到太阳辐射功率为
P_\text{in} = \frac{(1-a)\cdot S\cdot \pi R^2}{4\pi R^2} = \frac{(1-a) S}{4} \\
地球通过长波辐射向外太空输出的能量则可以通过将地球视为“黑体”来计算。斯特藩-玻尔兹曼定律(Stefan-Boltzman law)认为物体向外辐射的能量与其温度的四次方成正比。因此,地球表面单位面积上向外输出的功率为
P_\text{out} = \varepsilon \sigma T^4 \\
其中 \sigma = 5.67 \times 10-8 W/m2/K4 为斯特藩-玻尔兹曼常数。\varepsilon 为表面的发射率,对于完美的黑体 \varepsilon = 1。T 为地球表面温度(以 K 为单位)。冰的发射率为 0.97,水的发射率为 0.96,水和冰几乎是完美的黑体。输入和输出能量通量之间的差被称为辐射强迫,并表示为
\Delta F = P_\text{in} - P_\text{out} = \frac{(1-a) S}{4} - \varepsilon \sigma T^4 \\
如果 \Delta F = 0,地球的温度就达到了平衡,地球的平衡温度为
T_0 = \left[\frac{(1-a) S}{4\varepsilon \sigma}\right]^{1/4} \\
如果不考虑温室效应,地球接近于完美黑体,此时 \varepsilon = 1。将 a = 0.3,S = 1370 W/m2 和 \sigma = 5.67 \times 10-8 W/m2/K4 代入上式可得 T_0 = 255 K = -18 ℃。也就是说,如果完全没有温室效应,地表的平均温度大约为 - 18 ℃。但由于正常的温室效应,有效发射率 \varepsilon < 1。如果以 1951-1980 年地表平均温度 T_0 = 14.2 ℃ = 287.35 K 为参考点(即认为这个温度是正常温室效应的结果),据此可推算出地球的有效发射率为 \varepsilon = 0.6246。从上面的分析中可以看出,人类的生存和发展其实也得益于温室效应。如果没有温室效应,地球将处于冰封之中。
但由于大气中的 CO2 等温室气体的浓度越来越高,温室效应越来越强。温室气体捕获了部分本应辐射到外太空的能量,导致 \Delta F > 0。即地球从太阳获得到热量大于了地球向外辐射的热量。为了继续维持平衡,地球不得不从 T_0 升高温度 \Delta T 来向外多辐射 \Delta F 的热量:
\begin{aligned} \Delta F &= \varepsilon \sigma (T_0+\Delta T)^4 - \frac{(1-a) S}{4}\\ &= \varepsilon \sigma T_0^4 \left(1 +\frac{\Delta T}{T_0}\right)^4 - \frac{(1-a) S}{4} \end{aligned}\\
将 \varepsilon \sigma T_0^4 = (1-a)S/4 代入上式可得
\Delta F = \frac{(1-a) S}{4}\left[\left(1 +\frac{\Delta T}{T_0}\right)^4 - 1\right] \\
考虑到 \Delta T/T_0\ll 1,上式中的 (1 + \Delta T/T_0)^4 可展开并近似为
\begin{aligned} \left(1 +\frac{\Delta T}{T_0}\right)^4 & = 1 + 4\left(\frac{\Delta T}{T_0}\right) + 6\left(\frac{\Delta T}{T_0}\right)^2 + 4\left(\frac{\Delta T}{T_0}\right)^3 + \left(\frac{\Delta T}{T_0}\right)^4\\ &\approx 1 + 4\left(\frac{\Delta T}{T_0}\right) \end{aligned}\\
因此有
\Delta F \approx \frac{(1-a)S}{T_0}\, \Delta T\quad\text{或}\quad \Delta T \approx \frac{T_0}{(1-a)S}\, \Delta F \\
也就是说,辐射强迫 \Delta F 和温度增量 \Delta T 存在近似的线性关系。
研究表明,CO2 从参考浓度 C_0 增加到 C 所引起的辐射强迫可以通过以下公式计算[9]:
\Delta F_{\text{CO}_2} = 5.35\ln\left(\frac{C}{C_0}\right) \\
上式中的 CO2 参考浓度 C_0 表示参考气温 T_0 所对应 CO2 浓度,也就是 1951-1980 年大气中 CO2 的平均浓度,其数值大约为 320 ppm 左右。考虑到人类活动排放的其它温室气体应该与排放的 CO2 正相关,本文假设(包括其它温室气体造成的)总的辐射强迫 \Delta F 与 CO2 造成的辐射强迫 \Delta F_{\text{CO}_2} 成正比,即
\Delta F = \eta\, \Delta F_{\text{CO}_2} =5.35\,\eta\,\ln\left(\frac{C}{C_0}\right) \\
其中 \eta 为常数。将上式代到温度异常 \Delta T 的表达式中可得
\begin{aligned} \Delta T &\approx \frac{5.35\,\eta\,T_0}{(1-a)S} \ln\left(\frac{C}{C_0}\right) \\ &= \frac{5.35\times 287.35\,\eta}{(1-0.3)\times 1370}\,\ln\left(\frac{C}{C_0}\right)\\ & = 1.603\,\eta \,\ln\left(\frac{C}{C_0}\right) \end{aligned}\\
其中 \eta 和 C_0 均为常数。上式给出了地表平均温度异常 \Delta T 与大气中的 CO2 浓度 C 的关系,我们可以直接使用该函数关系对 CO2 浓度和温度异常进行拟合。通过拟合得到上式中的 \eta = 2.3556、C_0 = 324.5,拟合曲线如图 8 所示。
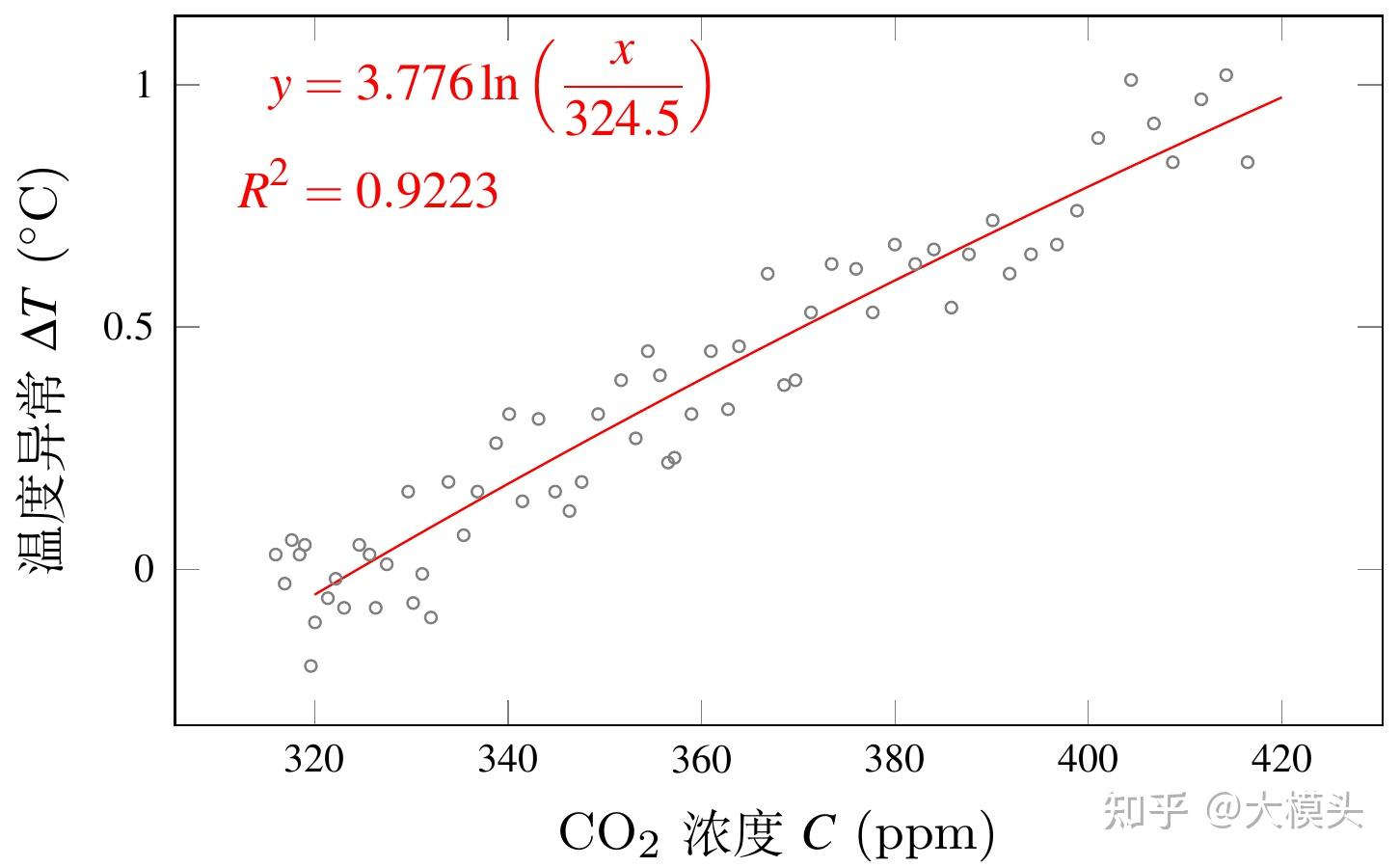
图 8: 二氧化碳浓度与温度的关系拟合
预测更大浓度 CO2 导致的温度异常可以通过延长该曲线获得(图 9)。预测特定 CO2 浓度导致的温度异常比预测特定年份的温度异常更有意义:一方面,未来 CO2 浓度具有不确定性,它依赖于人类当前和未来的碳排放策略;另一方面,这种预测能够告诉我们 CO2 浓度在哪个值以下才能确保全球温度的升高在某个值以内。这可以为各国制定碳排放策略提供依据。例如,如果我们要将全球地表平均温度升高控制在 2 ℃ 以下,就必需确保大气中的 CO2 浓度不超过 551 ppm(图 9)。

图 9: 二氧化碳特定浓度下的温度预测
如果把之前根据数据拟合得到的 CO2 浓度关于时间的指数函数 C(t) 代入到 \Delta T (C) 的表达式中,就可以得到温度异常 \Delta T 关于时间 t 的函数,由此可预测未来各年的温度异常。
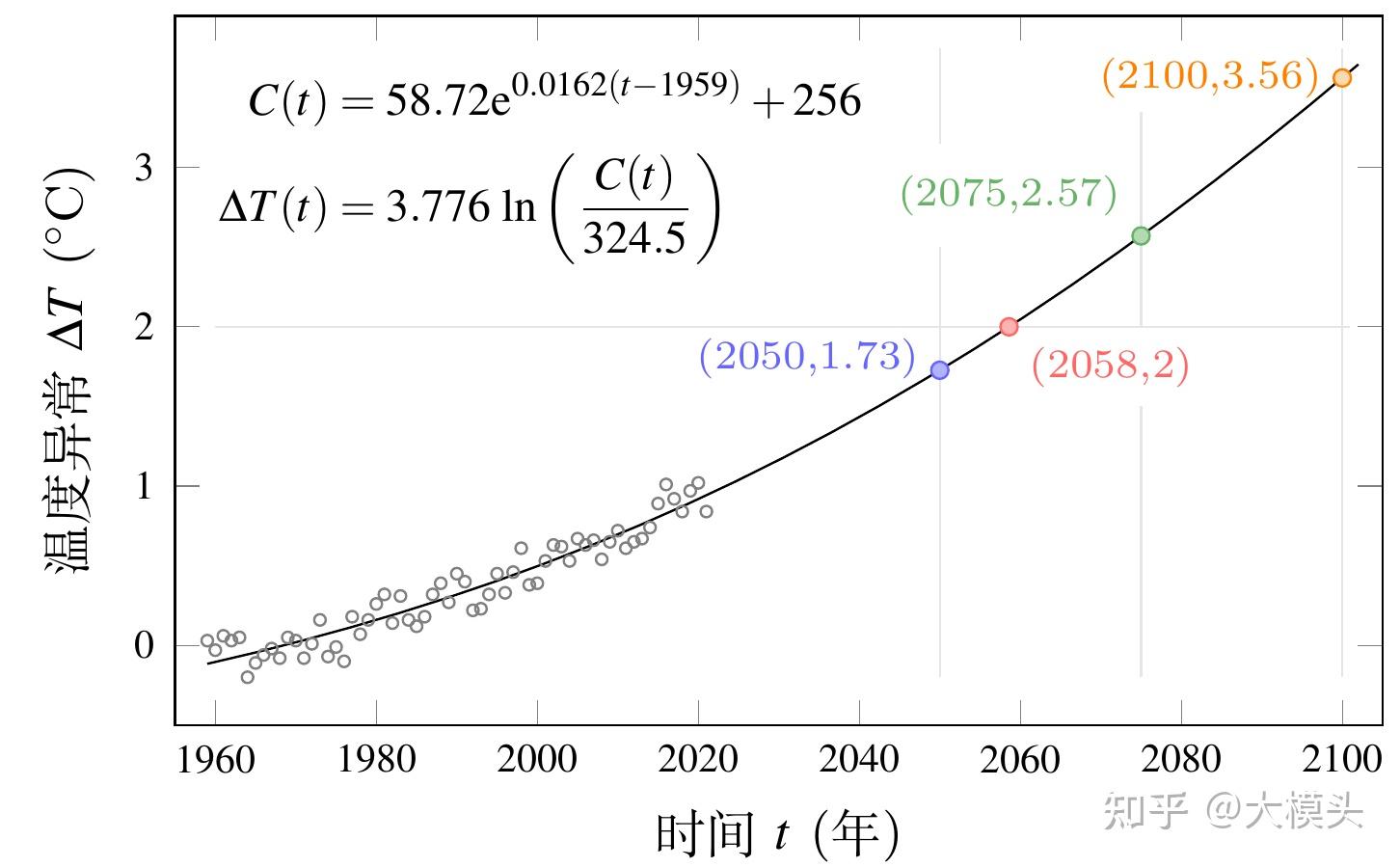
图 10: 未来年份的温度预测
预测结果如图 10 所示,如果人类不作出任何改变,那么 2050、2075 和 2100 年的全球平均温度异常将分别达到 1.73、2.57 和 3.56 ℃,全球平均温度异常将在 2058 年达到 2 ℃。
结论
自工业革命以来,大气中以 CO2 为代表的温室气体浓度不断上升,导致温室效应不断加强,全球气温也随之增加。本文通过建立数学模型预测了未来 CO2 浓度,以及温室效应导致的全球升温。
本文对 CO2 浓度的历史数据进行了指数拟合,并应用拟合得到的指数模型对未来的 CO2 浓度进行了预测。结果表明,如果大气中的 CO2 浓度继续以目前的趋势增长,那么 CO2 浓度将在 2050、2075 和 2100 年分别达到 512.7、641.0 和 833.3 ppm,并于 2060 年达到工业化前的两倍。为了将地表平均温度与大气中的 CO2 浓度联系起来,本文建立了地球能量平衡模型。在该模型中,地表平均温度由地球从太阳辐射获得的能量与地球向外太空辐射出去的能量相互平衡来确定,温室气体的作用被考虑为辐射强迫。模型结果表明,地表平均温度异常是 CO2 浓度的对数函数。据此,本文对大气中的 CO2 浓度和全球地表平均温度进行了拟合,并对未来更大浓度二氧化碳导致的温度变化进行了预测。结果表明,如果大气中的 CO2 浓度继续以目前的趋势增长,地表平均温度将于 2050、2075 和 2100 年分别超出 1951-1980 年的均值 1.73、2.57 和 3.56 ℃。
科学研究清楚地表明,为了避免气候变化出现最严重的影响,保护宜居的地球,需要将全球气温上升限制在不超过工业化前水平 1.5 ℃ 的范围内[10]。但本文的研究结果表明,如果人类不立即、迅速并大规模地减少温室气体的排放,几乎不太可能将全球升温限制在 1.5 ℃ 以内。
参考资料
[1] United Nations-Climate Action. What is climate change?, 2022: https://www.un.org/en/climatechange/what-is-climate-change
[2] Wikipedia. Greenhouse effect, 2022: https://en.wikipedia.org/wiki/Greenhouse_effect
[3] NASA. Giss surface temperature analysis, 2022: https://data.giss.nasa.gov/gistemp
[4] Pieter Tans and Ralph Keeling. Trends in atmospheric carbon dioxide, 2021: https://gml.noaa.gov/ccgg/trends/data.html
[5] D. J. Hofmann, J. H. Butler, and P. P. Tans. A new look at atmospheric carbon dioxide. Atmospheric Environment, 43(12):2084–2086, 2009
[6] AD Hüsler and D. Sornette. Evidence for super-exponentially accelerating atmospheric carbon dioxide growth, 2011
[7] Michael Mann. Simple climate models, 2022: https://www.e-education.psu.edu/meteo469/node/137
[8] Chemistry for Life. Climate sensitivity, 2022: https://www.acs.org/content/acs/en/climatescience/atmosphericwarming/climatsensitivity.html
[9] Wikipedia. Radiative forcing, 2022: https://en.wikipedia.org/wiki/Radiative_forcing
[10] United Nations-Climate Action. For a livable climate: Net-zero commitments must be backed by credible action, 2022: https://www.un.org/en/climatechange/net-zero-coalition |
|