|
|
这篇论文是首个在large-scale数据集(比如ImageNet)上评估二值神经网络的工作。本文提出了两种二值神经网络:
- Binary-Weight-Networks:只有权重是二值化的,相比全精度网络节省32x的内存占用。
- XNOR-Networks:权重和激活值都是二值化的,可以将卷积运算转化为 XNOR 和 Bitcount 运算,从高精度运算次数的角度来说,可以为网络提供58x的加速。
<hr/>有关二值神经网络的基本知识,如XNOR、bitcount等概念,可参考
XNOR-Net实现代码:1-论文版本, 2-Pytorch版本
<hr/>权重的二值化
1. 二值权重网络的卷积 在CNN中,我们用W \in \mathscr{R}^{c \times w \times h}来表示一个filter中的权重,它的值是real-value的,在二值神经网络(BNN)中,我们用二值filter权重B \in \mathscr{R}^{c \times w \times h}和一个尺度因子\alpha来近似W,W \approx \alpha B,那么CNN原本的卷积就可以写为如下BNN的卷积: I*W \approx (I\oplus B)\alpha \tag{1} 其中I表示输入,因为B是二值的,所以 \oplus 运算只包含加法和减法,没有乘法。原本的网络参数是32-float类型,转化为二值之后,节约了大约32X的内存空间。
2. 最优的二值化参数 问题是怎么找到最优的二值化参数B,使得W \approx \alpha B成立呢?不失一般性,我们这里假设W和B都是n维的向量,其中n=c \times w \times h,我们要优化的函数如下所示: J(B,\alpha)=min(||W-\alpha B||^2) \tag{2} 展开式2可得: J(B,\alpha)=min(\alpha^2B^TB-2\alpha W^TB+W^TW) \tag{3}因为B \in {+1,-1}^n,所以 B^TB=n 是一个常数;因为 W 是已知的,所以W^TW也是一个常数,我们令其为c。现在式3可以重新表达为J(B,\alpha)=min(\alpha^2 n-2\alpha W^TB+c)。式2中的\alpha是正数,n和c是常数,因此我们想找的最优的二值化参数满足: B^*=argmax(W^TB), s.t. B\in\{+1,-1\}^n \tag{4}很明显,当W_i\geq 0时,B_i=+1,当W_i<0时,B_i=-1,这样的优化方法可以使得W^TB最大。我们用表达式B^=sign(W)来表示。 为了求得最优的\alpha,我们求J(B,\alpha)对\alpha的导数,并令其等于零,可得: \alpha^*=\frac{W^TB^*}{n} \tag{5}用 sign(W)替换 B^* ,式5可写为: \alpha^*=\frac{W^T sign(W)}{n}=\frac{\sum{|W_i|}}{n}=\frac{1}{n}||W||_{l1} \tag{6}
3. 二值权重网络的反向传播: 二值权重网络的反向传播需要计算sign()函数的梯度,我们将sign(r)的梯度近似为\frac{\partial sign}{\partial r}=1_{|r|\leq 1}。反向传播时,损失函数对权重的导数,指的是对二值权重的导数,但是在更新权重的时候,要更新real-value的权重。因为在梯度下降中,参数的改变量很小,更新了参数之后再二值化会忽略掉这些改变,所以在反向传播的过程中要一直保留real-value的权重,并保持对它的更新。一旦模型训练结束,在inference过程中,就只保留二值的网络参数即可。Algorithm 1是训练二值权重网络的过程。

XNOR-Net,权重和输入都二值化的网络
当只有权重是二值的时候,卷积中只包含加减法,只有将输入也变成二值的,才能在卷积中使用XNOR(同或)和Bitcount运算。 那如何用二值化的tensor来近似两个tensor的点乘呢,我们需要找到最优的对输入的二值化函数和尺度因子。假设我们要计算W,B \in \mathscr{R}^{n}之间的点乘,可以对其近似W^TB\approx \beta H^T \alpha B,其中W,B\in {-1,+1}^n,\alpha , \beta \in \mathscr{R}^{+},我们需要优化如下函数: \alpha^*,B^*,\beta^*,H^*=argmin||W\odot B-\beta\alpha H\odot B|| \tag{7} 其中\odot表示元素乘,令Y\in \mathscr{R}^{n},使得Y_i=X_iW_i,令C\in {+1,-1}^{n},使得C_i=H_iB_i,令\gamma \in \mathscr{R}^{+},使得\gamma=\alpha\beta,公式(7)即可写为: \gamma^*,Y^*=argmin||Y-\gamma C|| \tag{8} 推理过程如同公式(2)一样,可得: C^*=sign(Y)=sign(X)\odot sign(W)=H^*\odot B^* \tag{9} 因为|X_i|,|W_i|是独立的,且Y_i=X_iW_i,可得:E[|Y_i|]=E[|X_i|]E[|W_i|],因此: \gamma^*=\frac{\sum{|Y_i|}}{n}=\frac{\sum{|X_i||W_i|}}{n}\approx (\frac{1}{n}||X||_{l1})(\frac{1}{n}||W||_{l1})=\beta^*\alpha^* \tag{10}
二值卷积提升效率的方法: 给定了卷积核W\in\mathscr{R}^{c\times w\times h}和输入I \in \mathscr{R}^{c\times w_{in} \times h_{in}}计算卷积过程中,卷积核每移动一个地方,都需要计算相应位置卷积核的大小内计算输入元素的\beta,因此在卷积核的移动过程中,有很多的overlap区域会被多次重复计算。 为了避免这些冗余计算,首先计算输入I在通道上的绝对值的均值矩阵A=\frac{\sum{|I_{:,:,i}|}}{c},之后用一个卷积核k\in\mathscr{R}^{w\times h}, \forall_{ij}, k_{ij}=\frac{1}{w\times h}来对输入I进行卷积,得K=A*k,K包含了输入I所有可能的局部tensor的尺度因子\beta,K_{ij}对应的以输入I_{ij}为中心的\beta,因此卷积运算可写为: I*W\approx (sign(I)\circ sign(W))\odot K\alpha \tag{11} 其中,\circ表示XNOR和bitcount运算。 网络结构的不同 CNN网络的结构顺序为1-Conv、2-Norm、3-激活、4-pool,在二值网络中,使用sign()函数作为非线性层,如果把max-pool放在sign()激活之后,那么得到的结果就是大部分都是+1的tensor,因此需要给网络结构调整为:1-Norm、2-BinAct、3-BinConv、4-Pool。在BinConv后也可以插入一个非线性层如ReLU,来适应主流的网络架构如VGG。
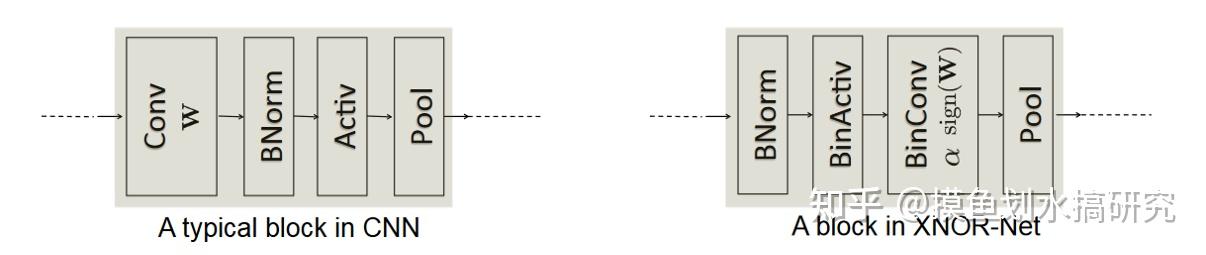
网络结构
<hr/>参考文献
XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks |
|